《2025年暑假作业知识出版社八年级数学华师大版》

6. 如图,点 $E$、$F$、$G$、$H$ 分别是平行四边形 $ABCD$ 各边的中点,连结 $AF$、$CE$ 相交于点 $M$,连结 $AG$、$CH$ 相交于点 $N$. 求证：四边形 $AMCN$ 是平行四边形.
证明：∵点 $E$、$F$、$G$、$H$ 分别是平行四边形 $ABCD$ 各边的中点，
∴ $AH// CF$，$AH=CF$，
∴ 四边形 $AFCH$ 是平行四边形，
∴ $AM// CN$.
同理可得，四边形 $AECG$ 是平行四边形，∴ $AN// CM$，∴ 四边形 $AMCN$ 是平行四边形.

答案： 证明 $\because$ 点 $E$、$F$、$G$、$H$ 分别是平行四边形 $ABCD$ 各边的中点，
$\therefore AH// CF$，$AH=CF$，
$\therefore$ 四边形 $AFCH$ 是平行四边形，
$\therefore AM// CN$.
同理可得，四边形 $AECG$ 是平行四边形，$\therefore AN// CM$，$\therefore$ 四边形 $AMCN$ 是平行四边形.

7. 综合实践课上,嘉嘉画出$\triangle ABD$,利用尺规作图找一点 $C$,使得四边形 $ABCD$ 为平行四边形,图 1～图 3 是其作图过程.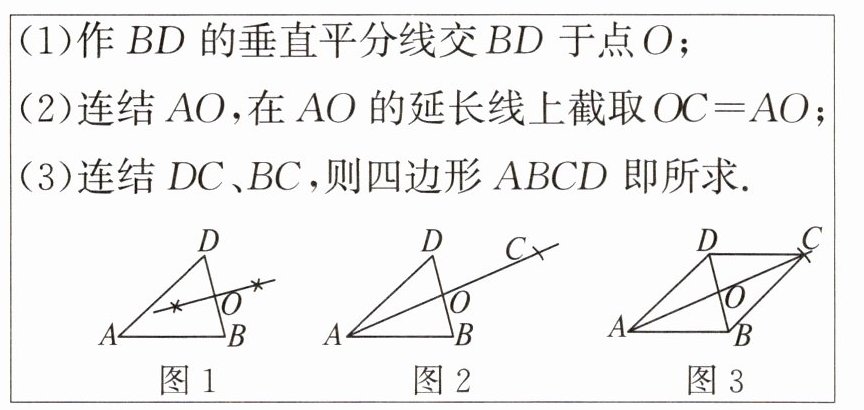
在嘉嘉的作法中,可直接判定四边形 $ABCD$ 为平行四边形的条件是(C)
A. 两组对边分别平行 B. 两组对边分别相等
C. 对角线互相平分 D. 一组对边平行且相等

答案： C

8. 如图,在方格图中,线段 $PQ$ 的两个端点都在格点上,方格图中另有 $A$、$B$、$C$、$D$ 四个格点,下面四个结论中,正确的是(B)

A. 连结 $AB$,则 $AB// PQ$ B. 连结 $BC$,则 $BC// PQ$
C. 连结 $BD$,则 $BD\perp PQ$ D. 连结 $AD$,则 $AD\perp PQ$

答案： B