《2025年暑假作业知识出版社八年级数学华师大版》

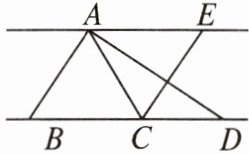
10. 如图,直线$AE// BD$,四边形$ABCE$为平行四边形,点$C在BD$上,若$AE = 5$,$BD = 8$,$\triangle ABD$的面积为 16,则$\triangle ABC$的面积为______10.

答案： 10

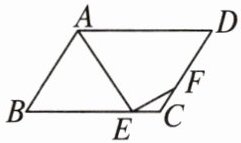
11. 如图,在$□ ABCD$中,$AD = 2AB$,点$E为AD$的中点,$CE的延长线交BA的延长线于点F$.
(1)求证：$FB = AD$；
(2)若$\angle DAF = 70^{\circ}$,求$\angle EBC$的度数.

(1) 证明 $\because E$ 为 $AD$ 的中点，
$\therefore DE = AE$。
$\because$ 四边形 $ABCD$ 是平行四边形，
$\therefore AB// CD$，$AB = DC$，$AD = BC$，
$\therefore\angle EDC = \angle EAF$。
在 $\triangle DEC$ 和 $\triangle AEF$ 中，
$\begin{cases}\angle DEC = \angle AEF, \\DE = AE, \\\angle EDC = \angle EAF,\end{cases}$
$\therefore\triangle DEC\cong\triangle AEF$，$\therefore DC = AF$。
$\because AD = 2AB$，$\therefore AB = DE = EA = AF$，
$\therefore AF + AB = 2AB$，即 $FB = AD$。
(2) 解 $\because$ 四边形 $ABCD$ 是平行四边形，
$\therefore DA// CB$，$\therefore\angle CBF = \angle DAF = 70^{\circ}$，$\angle AEB = \angle EBC$，又由 (1) 知 $AE = AB$，
$\therefore\angle AEB = \angle ABE=\frac{1}{2}\angle DAF$，
$\therefore\angle EBC = \angle ABE = 35°$。

答案：
(1) 证明 $\because E$ 为 $AD$ 的中点，
$\therefore DE = AE$。
$\because$ 四边形 $ABCD$ 是平行四边形，
$\therefore AB// CD$，$AB = DC$，$AD = BC$，
$\therefore\angle EDC = \angle EAF$。
在 $\triangle DEC$ 和 $\triangle AEF$ 中，
$\begin{cases}\angle DEC = \angle AEF, \\DE = AE, \\\angle EDC = \angle EAF,\end{cases}$
$\therefore\triangle DEC\cong\triangle AEF$，$\therefore DC = AF$。
$\because AD = 2AB$，$\therefore AB = DE = EA = AF$，
$\therefore AF + AB = 2AB$，即 $FB = AD$。
(2) 解 $\because$ 四边形 $ABCD$ 是平行四边形，
$\therefore DA// CB$，$\therefore\angle CBF = \angle DAF = 70^{\circ}$，$\angle AEB = \angle EBC$，又由
(1) 知 $AE = AB$，
$\therefore\angle AEB = \angle ABE=\frac{1}{2}\angle DAF$，
$\therefore\angle EBC = \angle ABE = 35^{\circ}$。

12. 如图,在$□ ABCD$中,$AE平分\angle BAD交BC于点E$,过点$E作AE的垂线交CD于点F$. 若$CF = 1$,$AD = 5$,求$AB$的长.

解 $\because$ 四边形 $ABCD$ 是平行四边形，
$\therefore AD// BC$，$\angle BAD = \angle C$，$AD = BC = 5$，$\therefore\angle DAE = \angle AEB$，
又 $\because AE$ 平分 $\angle BAD$，
$\therefore\angle BAE = \angle DAE$，
$\therefore\angle AEB = \angle BAE$，$\therefore BE = AB$。
设 $\angle BAE = x$，则 $\angle C = \angle BAD = 2x$，$\angle B = 180^{\circ} - 2x$。
$\because AE\perp EF$，$\therefore\angle AEF = 90^{\circ}$，
$\therefore\angle FEC = 90^{\circ} - x$，
$\because\angle EFC = 180^{\circ} - (\angle C + \angle CEF) = 180^{\circ} - (2x + 90^{\circ} - x) = 90^{\circ} - x$，
$\therefore\angle FEC = \angle EFC$，$\therefore CF = CE = 1$，
$\therefore BE = 4$，$\therefore AB =$4。

答案： 解 $\because$ 四边形 $ABCD$ 是平行四边形，
$\therefore AD// BC$，$\angle BAD = \angle C$，$AD = BC = 5$，$\therefore\angle DAE = \angle AEB$，
又 $\because AE$ 平分 $\angle BAD$，
$\therefore\angle BAE = \angle DAE$，
$\therefore\angle AEB = \angle BAE$，$\therefore BE = AB$。
设 $\angle BAE = x$，则 $\angle C = \angle BAD = 2x$，$\angle B = 180^{\circ} - 2x$。
$\because AE\perp EF$，$\therefore\angle AEF = 90^{\circ}$，
$\therefore\angle FEC = 90^{\circ} - x$，
$\because\angle EFC = 180^{\circ} - (\angle C + \angle CEF) = 180^{\circ} - (2x + 90^{\circ} - x) = 90^{\circ} - x$，
$\therefore\angle FEC = \angle EFC$，$\therefore CF = CE = 1$，
$\therefore BE = 4$，$\therefore AB = 4$。