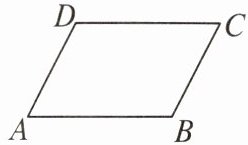
1. 如图,在四边形 $ABCD$ 中,$BC// AD$,添加下列条件,不能判定四边形 $ABCD$ 是平行四边形的是(
A. $AB = CD$ B. $AB// CD$ C. $\angle A= \angle C$ D. $BC = AD$
A
)
A. $AB = CD$ B. $AB// CD$ C. $\angle A= \angle C$ D. $BC = AD$
答案:
A
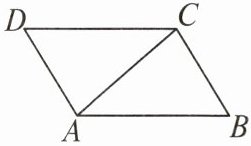
2. 如图,在$□ ABCD$中,连结 $AC$,已知$\angle BAC = 40^{\circ}$,$\angle ACB = 80^{\circ}$,则$\angle BCD= $(
A. $80^{\circ}$ B. $100^{\circ}$ C. $120^{\circ}$ D. $140^{\circ}$
C
)
A. $80^{\circ}$ B. $100^{\circ}$ C. $120^{\circ}$ D. $140^{\circ}$
答案:
C
3. 在$□ ABCD$中,$AD = 8$,$AE平分\angle BAD$交 $BC$ 于点 $E$,$DF平分\angle ADC$交 $BC$ 于点 $F$,且 $EF = 2$,则 $AB$ 的长为(
A. $3$ B. $4$或 $5$ C. $4$ D. $3$或 $5$
D
)A. $3$ B. $4$或 $5$ C. $4$ D. $3$或 $5$
答案:
D
4. 如图,小宇将一张平行四边形纸片折叠,使点 $A$ 落在长边 $CD$ 上的点 $A'$ 处,并得到折痕 $DE$,小宇测得长边 $CD = 8$,则四边形 $A'EBC$ 的周长为______

16
.
答案:
16
5. 如图,已知 $EF// AC$,$B$、$D$ 分别是 $AC$ 和 $EF$ 上的点,$\angle EDC= \angle CBE$.
求证:四边形 $BCDE$ 是平行四边形.
证明:$\because EF// AC$,
$\therefore \angle EDC+\angle BCD=180^{\circ }$,
又 $\because \angle EDC=\angle CBE$,
$\therefore \angle CBE+\angle BCD=180^{\circ }$,
$\therefore BE// CD$,又 $\because ED// BC$,$\therefore$ 四边形 $BCDE$ 是平行四边形.
求证:四边形 $BCDE$ 是平行四边形.
证明:$\because EF// AC$,
$\therefore \angle EDC+\angle BCD=180^{\circ }$,
又 $\because \angle EDC=\angle CBE$,
$\therefore \angle CBE+\angle BCD=180^{\circ }$,
$\therefore BE// CD$,又 $\because ED// BC$,$\therefore$ 四边形 $BCDE$ 是平行四边形.
答案:
证明 $\because EF// AC$,
$\therefore \angle EDC+\angle BCD=180^{\circ }$,
又 $\because \angle EDC=\angle CBE$,
$\therefore \angle CBE+\angle BCD=180^{\circ }$,
$\therefore BE// CD$,又 $\because ED// BC$,$\therefore$ 四边形 $BCDE$ 是平行四边形.
$\therefore \angle EDC+\angle BCD=180^{\circ }$,
又 $\because \angle EDC=\angle CBE$,
$\therefore \angle CBE+\angle BCD=180^{\circ }$,
$\therefore BE// CD$,又 $\because ED// BC$,$\therefore$ 四边形 $BCDE$ 是平行四边形.
查看更多完整答案,请扫码查看


