2025年假期作业八年级数学人教版山东美术出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期作业八年级数学人教版山东美术出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 计算:
(1) $\sqrt{8}\times\sqrt{\frac{1}{2}}+(\sqrt{2})^{0}$ (2) $(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})+(\sqrt{27}-\sqrt{12})\div\sqrt{3}$
(1) $\sqrt{8}\times\sqrt{\frac{1}{2}}+(\sqrt{2})^{0}$ (2) $(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})+(\sqrt{27}-\sqrt{12})\div\sqrt{3}$
答案:
(1)3
(2)3
(1)3
(2)3
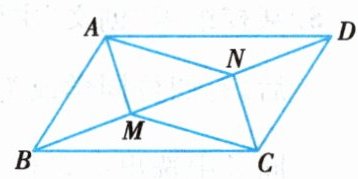
2. 如图,四边形 $ABCD$ 是平行四边形,$M、N$ 是对角线 $BD$ 上的两点,且 $BM = DN$. 求证:四边形 $AMCN$ 是平行四边形.

答案:
证明:如图,连接AC,交BD于点O.
∵四边形ABCD是平行四边形,
∴ $ OA = OC $, $ OB = OD $.
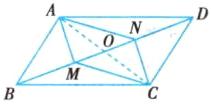
∵对角线BD上的两点M、N满足 $ BM = DN $,
∴ $ OB - BM = OD - DN $,即 $ OM = ON $,
∴四边形AMCN是平行四边形.
证明:如图,连接AC,交BD于点O.
∵四边形ABCD是平行四边形,
∴ $ OA = OC $, $ OB = OD $.

∵对角线BD上的两点M、N满足 $ BM = DN $,
∴ $ OB - BM = OD - DN $,即 $ OM = ON $,
∴四边形AMCN是平行四边形.
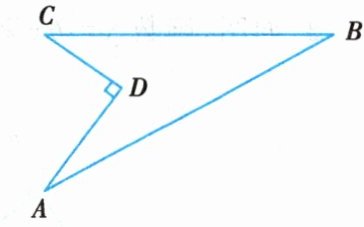
3. 如图,某住宅小区在施工过程中留下了一块空地,已知 $AD = 4$ 米,$CD = 3$ 米,$\angle ADC = 90^{\circ},AB = 13$ 米,$BC = 12$ 米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米 100 元,试问用草坪铺满这块空地共需花费多少元?

2400元
答案:
2400元
查看更多完整答案,请扫码查看


