2025年假期作业八年级数学人教版山东美术出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期作业八年级数学人教版山东美术出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如图所示的统计图和统计表.
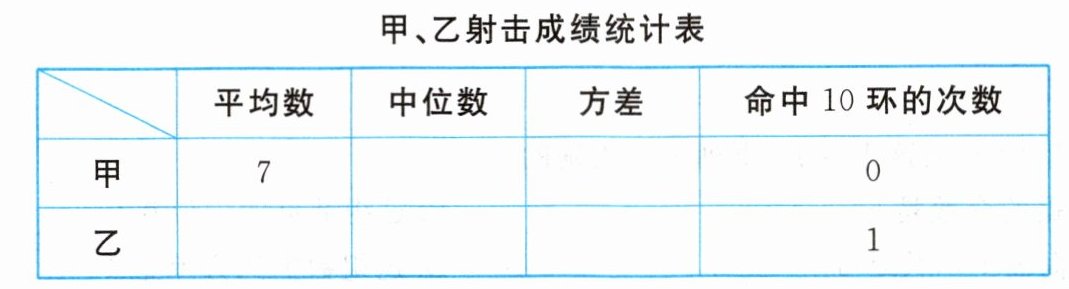

(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则? 为什么?


(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则? 为什么?
答案:
解:
(1) 根据折线统计图得乙的射击成绩为 2,4,6,8,7,7,8,9,9,10,则平均数为 $\frac{2 + 4 + 6 + 8 + 7 + 7 + 8 + 9 + 9 + 10}{10}=7$,中位数为 7.5,方差为 $\frac{1}{10}×[(2 - 7)^{2}+(4 - 7)^{2}+(6 - 7)^{2}+(8 - 7)^{2}+(7 - 7)^{2}+(7 - 7)^{2}+(8 - 7)^{2}+(9 - 7)^{2}+(9 - 7)^{2}+(10 - 7)^{2}]=5.4$;
由表知甲的射击成绩的平均数是 7,则甲第 8 次的射击成绩为 $70-(9 + 6 + 7 + 6 + 2 + 7 + 7 + 8 + 9)=9$ (环),故 10 次射击成绩为 2,6,6,7,7,7,8,9,9,9. 中位数为 7,方差为 $\frac{1}{10}×[(2 - 7)^{2}+(6 - 7)^{2}+(6 - 7)^{2}+(7 - 7)^{2}+(7 - 7)^{2}+(7 - 7)^{2}+(8 - 7)^{2}+(9 - 7)^{2}+(9 - 7)^{2}+(9 - 7)^{2}]=4$,补全图表如下:
甲、乙射击成绩统计表
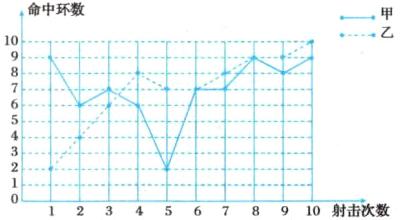
(2) 因为两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差,故甲胜出。
(3) 规定平均成绩高者胜出,若平均成绩相同,则随着比赛进行,发挥越来越好者胜出,可以让乙胜出。
解:
(1) 根据折线统计图得乙的射击成绩为 2,4,6,8,7,7,8,9,9,10,则平均数为 $\frac{2 + 4 + 6 + 8 + 7 + 7 + 8 + 9 + 9 + 10}{10}=7$,中位数为 7.5,方差为 $\frac{1}{10}×[(2 - 7)^{2}+(4 - 7)^{2}+(6 - 7)^{2}+(8 - 7)^{2}+(7 - 7)^{2}+(7 - 7)^{2}+(8 - 7)^{2}+(9 - 7)^{2}+(9 - 7)^{2}+(10 - 7)^{2}]=5.4$;
由表知甲的射击成绩的平均数是 7,则甲第 8 次的射击成绩为 $70-(9 + 6 + 7 + 6 + 2 + 7 + 7 + 8 + 9)=9$ (环),故 10 次射击成绩为 2,6,6,7,7,7,8,9,9,9. 中位数为 7,方差为 $\frac{1}{10}×[(2 - 7)^{2}+(6 - 7)^{2}+(6 - 7)^{2}+(7 - 7)^{2}+(7 - 7)^{2}+(7 - 7)^{2}+(8 - 7)^{2}+(9 - 7)^{2}+(9 - 7)^{2}+(9 - 7)^{2}]=4$,补全图表如下:
甲、乙射击成绩统计表

(2) 因为两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差,故甲胜出。
(3) 规定平均成绩高者胜出,若平均成绩相同,则随着比赛进行,发挥越来越好者胜出,可以让乙胜出。
2. 学校开展“书香校园”活动以来,受到同学们的广泛关注. 学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图所示的不完整的统计图表.
学生借阅图书的次数统计表
|借阅图书的次数|0次|1次|2次|3次|4次及以上|
|----|----|----|----|----|----|
|人数|7|13|
请你根据统计图表中的信息,解答下列问题:

(1)$a=$
(2)该调查统计数据的中位数是
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
学生借阅图书的次数统计表
|借阅图书的次数|0次|1次|2次|3次|4次及以上|
|----|----|----|----|----|----|
|人数|7|13|
17
|10|3|请你根据统计图表中的信息,解答下列问题:

(1)$a=$
17
,$b=$20
;(2)该调查统计数据的中位数是
2
,众数是2
;(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
答案:
(1) 17 20
(2) 2 2
(3) $72^{\circ}$
(4) 120
(1) 17 20
(2) 2 2
(3) $72^{\circ}$
(4) 120
查看更多完整答案,请扫码查看


