《2025年暑假作业中国地图出版社八年级数学》

学校开展了一次动漫设计大赛,小光同学运用数学知识进行了富有创意的图案设计。如图13,他在边长为1的正方形ABCD内作等边△BCE,并与正方形的对角线交于点F,G,制作成了如图14所示的图标。同学们,开动脑筋,相信你也能以正方形为背景设计出这样有创意的图案！


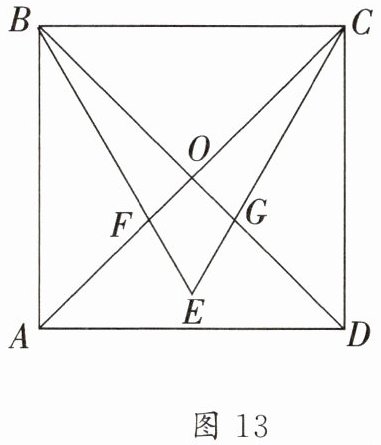
则图中阴影部分的面积是$\frac{3-\sqrt{3}}{6}$。

答案： 1. 首先求$\angle BAE$的度数：
因为四边形$ABCD$是正方形，所以$AB = BC$，$\angle ABC=\angle BAD = 90^{\circ}$。
又因为$\triangle BCE$是等边三角形，所以$BC = BE$，$\angle EBC = 60^{\circ}$。
那么$AB = BE$，$\angle ABE=\angle ABC-\angle EBC=90^{\circ}-60^{\circ}=30^{\circ}$。
在$\triangle ABE$中，$AB = BE$，根据等腰三角形的性质$\angle BAE=\angle BEA$。
由三角形内角和定理$\angle BAE+\angle BEA+\angle ABE = 180^{\circ}$，可得$\angle BAE=\frac{1}{2}(180^{\circ}-\angle ABE)=\frac{1}{2}(180 - 30)^{\circ}=75^{\circ}$。
2. 然后求$\angle FAE$的度数：
因为四边形$ABCD$是正方形，$AC$是对角线，所以$\angle BAC = 45^{\circ}$。
则$\angle FAE=\angle BAE-\angle BAC$。
把$\angle BAE = 75^{\circ}$，$\angle BAC = 45^{\circ}$代入可得$\angle FAE=75^{\circ}-45^{\circ}=30^{\circ}$。
3. 接着求$AE$的长度：
在$\triangle ABE$中，$AB = BE = 1$，$\angle ABE = 30^{\circ}$，过$E$作$EH\perp AB$于$H$。
在$Rt\triangle BEH$中，$BH=\frac{1}{2}BE=\frac{1}{2}$（$30^{\circ}$所对的直角边等于斜边的一半），$EH=\sqrt{BE^{2}-BH^{2}}=\sqrt{1 - (\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$。
因为$AH=AB - BH=1-\frac{1}{2}=\frac{1}{2}$。
在$Rt\triangle AEH$中，根据勾股定理$AE=\sqrt{AH^{2}+EH^{2}}=\sqrt{(\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}} = 1$。
4. 再求$\triangle AEF$的面积：
因为$\angle FAE = 30^{\circ}$，$\angle AHE = 90^{\circ}$，设$EF = x$，则$AF = 2x$（$30^{\circ}$所对的直角边等于斜边的一半）。
由勾股定理$AF^{2}=AE^{2}+EF^{2}$（这里$AE = 1$），即$(2x)^{2}=1^{2}+x^{2}$。
展开得$4x^{2}=1 + x^{2}$，移项得$4x^{2}-x^{2}=1$，$3x^{2}=1$，$x^{2}=\frac{1}{3}$，$x=\frac{\sqrt{3}}{3}$（$x\gt0$）。
$S_{\triangle AEF}=\frac{1}{2}AE\cdot EF\cdot\sin\angle AEF$，因为$\angle AEF = 150^{\circ}$，$\sin150^{\circ}=\frac{1}{2}$，$AE = 1$，$EF=\frac{\sqrt{3}}{3}$。
$S_{\triangle AEF}=\frac{1}{2}×1×\frac{\sqrt{3}}{3}×\frac{1}{2}=\frac{\sqrt{3}}{12}$。
同理$S_{\triangle DEG}=\frac{\sqrt{3}}{12}$。
$S_{\triangle AED}=\frac{1}{2}×1×1=\frac{1}{2}$。
5. 最后求阴影部分面积$S$：
$S = S_{\triangle AED}-S_{\triangle AEF}-S_{\triangle DEG}$。
$S=\frac{1}{2}-2×\frac{\sqrt{3}}{12}=\frac{3 - \sqrt{3}}{6}$。
所以阴影部分的面积是$\frac{3-\sqrt{3}}{6}$。