《2025年暑假作业中国地图出版社八年级数学》

1. 满足下列条件的三角形中,不是直角三角形的是(D).
A.三内角之比为$1:2:3$
B.三边长的平方之比为$1:2:3$
C.三边长之比为$3:4:5$
D.三内角之比为$3:4:5$

答案： D

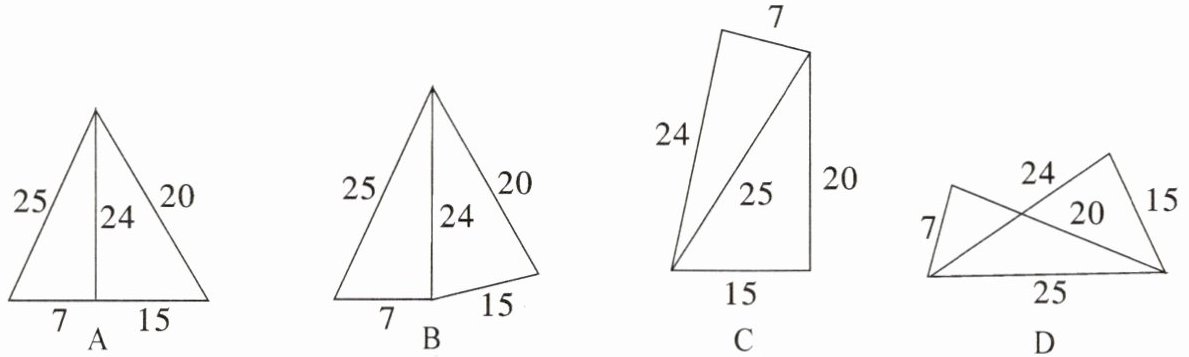
2. 已知五根小木棒的长度分别为$7$,$15$,$20$,$24$,$25$.现将它们摆成两个直角三角形,下列各图正确的是(C).

答案： C

3. 如图5,$E$,$F分别是正方形ABCD中BC和CD$边上的点,且$AB= 4$,$CE= \frac{1}{4}BC$,$F为CD$的中点,连接$AF$,$AE$,则$\triangle AEF$是什么三角形？请说明理由.
由勾股定理得$AE^{2}=25$，$EF^{2}=5$，$AF^{2}=20$。
$\because AE^{2}=EF^{2}+AF^{2}$，
$\therefore \triangle AEF$是直角三角形。

答案： 由勾股定理得$AE^{2}=25$，$EF^{2}=5$，$AF^{2}=20$。
$\because AE^{2}=EF^{2}+AF^{2}$，
$\therefore \triangle AEF$是直角三角形。