2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 已知函数 $ y _ { 1 } = - x + 3 $,$ y _ { 2 } = 3 x - 4 $,当 $ x $ 取何值时 $ y _ { 1 } > y _ { 2 } $?
$x<\frac{7}{4}$
当 $ x $ 取何值时 $ y _ { 1 } = y _ { 2 } $?$x=\frac{7}{4}$
当 $ x $ 取何值时 $ y _ { 1 } < y _ { 2 } $?$x>\frac{7}{4}$
答案:
$x<\frac{7}{4}$时,$y_1>y_2$;$x=\frac{7}{4}$,$y_1=y_2$;$x>\frac{7}{4}$时,$y_1<y_2$。
11. 解不等式组 $ \left\{ \begin{array} { l } { 5 > 2 ( 1 - x ), } \\ { - \frac { 1 } { 3 } \leq \frac { 2 } { 3 } - x, } \end{array} \right. $ 并算出该不等式组的整数解的和。
答案:
【解析】:
1. 首先解不等式$5\gt2(1 - x)$:
去括号:根据乘法分配律$a(b - c)=ab - ac$,可得$5\gt2 - 2x$。
移项:将含$x$的项移到一边,常数项移到另一边,得到$2x\gt2 - 5$。
计算:$2x\gt - 3$。
系数化为$1$:两边同时除以$2$,解得$x\gt-\frac{3}{2}$。
2. 然后解不等式$-\frac{1}{3}\leq\frac{2}{3}-x$:
移项:将$x$移到左边,常数项移到右边,得到$x\leq\frac{2}{3}+\frac{1}{3}$。
计算:$x\leq1$。
3. 接着求不等式组的解集:
因为不等式组$\begin{cases}x\gt-\frac{3}{2}\\x\leq1\end{cases}$,根据“大小小大中间找”的原则,所以不等式组的解集为$-\frac{3}{2}\lt x\leq1$。
4. 最后求不等式组的整数解及其和:
在$-\frac{3}{2}\lt x\leq1$这个范围内的整数有$-1$,$0$,$1$。
它们的和为$( - 1)+0 + 1=0$。
【答案】:不等式组的解集为$-\frac{3}{2}\lt x\leq1$,整数解的和为$0$。
1. 首先解不等式$5\gt2(1 - x)$:
去括号:根据乘法分配律$a(b - c)=ab - ac$,可得$5\gt2 - 2x$。
移项:将含$x$的项移到一边,常数项移到另一边,得到$2x\gt2 - 5$。
计算:$2x\gt - 3$。
系数化为$1$:两边同时除以$2$,解得$x\gt-\frac{3}{2}$。
2. 然后解不等式$-\frac{1}{3}\leq\frac{2}{3}-x$:
移项:将$x$移到左边,常数项移到右边,得到$x\leq\frac{2}{3}+\frac{1}{3}$。
计算:$x\leq1$。
3. 接着求不等式组的解集:
因为不等式组$\begin{cases}x\gt-\frac{3}{2}\\x\leq1\end{cases}$,根据“大小小大中间找”的原则,所以不等式组的解集为$-\frac{3}{2}\lt x\leq1$。
4. 最后求不等式组的整数解及其和:
在$-\frac{3}{2}\lt x\leq1$这个范围内的整数有$-1$,$0$,$1$。
它们的和为$( - 1)+0 + 1=0$。
【答案】:不等式组的解集为$-\frac{3}{2}\lt x\leq1$,整数解的和为$0$。
12. 如图所示,已知 $ □ ABCD $ 中,$ DE $ 是 $ \angle ADC $ 的角平分线,交 $ BC $ 于点 $ E $。
(1) 证明:$ CD = CE $;
(2) 若 $ BE = CE $,$ \angle B = 80 ^ { \circ } $,求 $ \angle DAE $ 的度数。
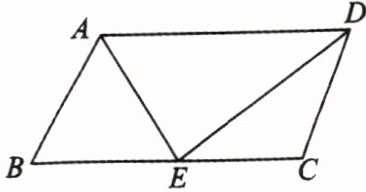
(1) 证明:因为四边形$ABCD$是平行四边形,所以$AD// BC$,可得$\angle ADE=\angle DEC$。又因为$DE$是$\angle ADC$的角平分线,所以$\angle ADE = \angle CDE$,从而$\angle DEC=\angle CDE$,根据等角对等边,所以$CD = CE$。
(2)
(1) 证明:$ CD = CE $;
(2) 若 $ BE = CE $,$ \angle B = 80 ^ { \circ } $,求 $ \angle DAE $ 的度数。

(1) 证明:因为四边形$ABCD$是平行四边形,所以$AD// BC$,可得$\angle ADE=\angle DEC$。又因为$DE$是$\angle ADC$的角平分线,所以$\angle ADE = \angle CDE$,从而$\angle DEC=\angle CDE$,根据等角对等边,所以$CD = CE$。
(2)
$50^{\circ}$
答案:
【解析】:
### $(1)$ 证明$CD = CE$
- 因为四边形$ABCD$是平行四边形,根据平行四边形的性质:平行四边形的对边平行,所以$AD// BC$。
- 由$AD// BC$,根据两直线平行,内错角相等,可得$\angle ADE=\angle DEC$。
- 又因为$DE$是$\angle ADC$的角平分线,所以$\angle ADE = \angle CDE$。
- 从而$\angle DEC=\angle CDE$。
- 根据等角对等边,所以$CD = CE$。
### $(2)$ 求$\angle DAE$的度数
- 因为四边形$ABCD$是平行四边形,所以$AB = CD$,$AD// BC$。
- 由$(1)$知$CD = CE$,且$BE = CE$,所以$AB = BE$。
- 因为$AB = BE$,$\angle B = 80^{\circ}$,根据等腰三角形的性质:等腰三角形两底角相等,以及三角形内角和为$180^{\circ}$,可得$\angle BAE=\angle BEA=\frac{1}{2}(180^{\circ}-\angle B)=\frac{1}{2}(180 - 80)^{\circ}=50^{\circ}$。
- 因为$AD// BC$,根据两直线平行,同旁内角互补,所以$\angle B+\angle BAD = 180^{\circ}$,则$\angle BAD=180^{\circ}-\angle B = 180 - 80^{\circ}=100^{\circ}$。
- 那么$\angle DAE=\angle BAD-\angle BAE=100^{\circ}-50^{\circ}=50^{\circ}$。
【答案】:
$(1)$ 证明过程如上述解析;$(2)$$\boldsymbol{50^{\circ}}$
### $(1)$ 证明$CD = CE$
- 因为四边形$ABCD$是平行四边形,根据平行四边形的性质:平行四边形的对边平行,所以$AD// BC$。
- 由$AD// BC$,根据两直线平行,内错角相等,可得$\angle ADE=\angle DEC$。
- 又因为$DE$是$\angle ADC$的角平分线,所以$\angle ADE = \angle CDE$。
- 从而$\angle DEC=\angle CDE$。
- 根据等角对等边,所以$CD = CE$。
### $(2)$ 求$\angle DAE$的度数
- 因为四边形$ABCD$是平行四边形,所以$AB = CD$,$AD// BC$。
- 由$(1)$知$CD = CE$,且$BE = CE$,所以$AB = BE$。
- 因为$AB = BE$,$\angle B = 80^{\circ}$,根据等腰三角形的性质:等腰三角形两底角相等,以及三角形内角和为$180^{\circ}$,可得$\angle BAE=\angle BEA=\frac{1}{2}(180^{\circ}-\angle B)=\frac{1}{2}(180 - 80)^{\circ}=50^{\circ}$。
- 因为$AD// BC$,根据两直线平行,同旁内角互补,所以$\angle B+\angle BAD = 180^{\circ}$,则$\angle BAD=180^{\circ}-\angle B = 180 - 80^{\circ}=100^{\circ}$。
- 那么$\angle DAE=\angle BAD-\angle BAE=100^{\circ}-50^{\circ}=50^{\circ}$。
【答案】:
$(1)$ 证明过程如上述解析;$(2)$$\boldsymbol{50^{\circ}}$
查看更多完整答案,请扫码查看


