《2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版》

8. 如图,在$\triangle ABC$中,$D$,$E分别是AC$,$AB$上的点,$BD与CE交于点O$,给出下列四个条件：①$∠EBO= ∠DCO$；②$∠BEO= ∠CDO$；③$BE= CD$；④$OB= OC$。
(1)上述四个条件中,哪两个条件可判定$\triangle ABC$是等腰三角形(用序号写出所有情况)；①③，①④，②③，②④
(2)选(1)小题中的一种情形,说明$\triangle ABC$是等腰三角形。
下面以①③两个条件证明$\triangle ABC$是等腰三角形.
$\because \angle EBO = \angle DCO$，$BE = CD$，$\angle EOB = \angle DOC$，
$\therefore \triangle EOB \cong \triangle DOC(AAS)$。
$\therefore OB = OC$，$\therefore \angle OBC = \angle OCB$。
$\because \angle EBO = \angle DCO$，$\therefore \angle EBC = \angle DCB$。
$\therefore \triangle ABC$是等腰三角形。

答案： 解：（1）有①③，①④，②③，②④四种情况可判定$\triangle ABC$是等腰三角形；
（2）下面以①③两个条件证明$\triangle ABC$是等腰三角形.
$\because \angle EBO = \angle DCO$，$BE = CD$，$\angle EOB = \angle DOC$，
$\therefore \triangle EOB \cong \triangle DOC(AAS)$.
$\therefore OB = OC$，$\therefore \angle OBC = \angle OCB$.
$\because \angle EBO = \angle DCO$，$\therefore \angle EBC = \angle DCB$.
$\therefore \triangle ABC$是等腰三角形.

9. $\triangle ABC在平面直角坐标系xOy$中的位置如图所示。
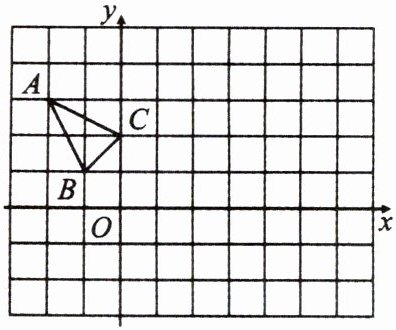
(1)作$\triangle ABC关于点C成中心对称的\triangle A_{1}B_{1}C_{1}$。连接$AC$并延长至$A_1$，使$CA_1 = AC$；连接$BC$并延长至$B_1$，使$CB_1 = BC$，连接$A_1B_1$、$B_1C$、$C A_1$，得到$\triangle A_{1}B_{1}C_{1}$
(2)将$\triangle A_{1}B_{1}C_{1}$向右平移3个单位长度,作出平移后的$\triangle A_{2}B_{2}C_{2}$。将$\triangle A_{1}B_{1}C_{1}$的各顶点$A_1$、$B_1$、$C_1$分别向右平移$3$个单位长度，得到$A_2$、$B_2$、$C_2$，连接$A_2B_2$、$B_2C_2$、$C_2A_2$，得到$\triangle A_{2}B_{2}C_{2}$

答案： 【解析】：
(1) 中心对称的性质是对应点连线经过对称中心，且被对称中心平分。
连接$AC$并延长至$A_1$，使$CA_1 = AC$；连接$BC$并延长至$B_1$，使$CB_1 = BC$，连接$A_1B_1$、$B_1C$、$C A_1$，得到$\triangle A_{1}B_{1}C_{1}$。
(2) 平移的性质是图形上的每个点都沿相同方向移动相同距离。
将$\triangle A_{1}B_{1}C_{1}$的各顶点$A_1$、$B_1$、$C_1$分别向右平移$3$个单位长度，得到$A_2$、$B_2$、$C_2$，连接$A_2B_2$、$B_2C_2$、$C_2A_2$，得到$\triangle A_{2}B_{2}C_{2}$。
【答案】：按上述方法作图即可（因无法直接绘制图形，故给出作图方法）。