2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如图,网格中的每个小正方形的边长都是1. 每个小正方形的顶点叫做格点.$△ACB和△DCE$的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:$△ACB\backsim △DCE$;
证明:(1)
(2)求证:$EF⊥AB$.
证明:(2)
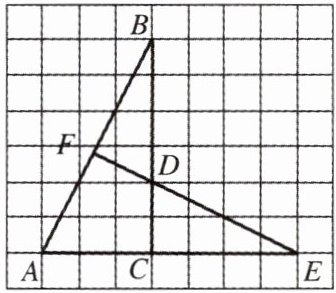
(1)求证:$△ACB\backsim △DCE$;
证明:(1)
$\because \frac{AC}{DC} = \frac{3}{2}$,$\frac{BC}{EC} = \frac{6}{4} = \frac{3}{2}$,$\therefore \frac{AC}{DC} = \frac{BC}{EC}$。又$∠ACB = ∠DCE = 90^{\circ}$,$\therefore △ACB \backsim △DCE$。
(2)求证:$EF⊥AB$.
证明:(2)
$\because △ACB \backsim △DCE$,$\therefore ∠ABC = ∠DEC$。又$∠ABC + ∠A = 90^{\circ}$,$\therefore ∠A + ∠DEC = 90^{\circ}$$\therefore ∠EFA = 90^{\circ}$。$\therefore EF⊥AB$。

答案:
证明:
(1)$\because \frac{AC}{DC} = \frac{3}{2}$,$\frac{BC}{EC} = \frac{6}{4} = \frac{3}{2}$,$\therefore \frac{AC}{DC} = \frac{BC}{EC}$。
又$∠ACB = ∠DCE = 90^{\circ}$,$\therefore △ACB \backsim △DCE$。
(2)$\because △ACB \backsim △DCE$,$\therefore ∠ABC = ∠DEC$。
又$∠ABC + ∠A = 90^{\circ}$,$\therefore ∠A + ∠DEC = 90^{\circ}$
$\therefore ∠EFA = 90^{\circ}$。$\therefore EF⊥AB$。
(1)$\because \frac{AC}{DC} = \frac{3}{2}$,$\frac{BC}{EC} = \frac{6}{4} = \frac{3}{2}$,$\therefore \frac{AC}{DC} = \frac{BC}{EC}$。
又$∠ACB = ∠DCE = 90^{\circ}$,$\therefore △ACB \backsim △DCE$。
(2)$\because △ACB \backsim △DCE$,$\therefore ∠ABC = ∠DEC$。
又$∠ABC + ∠A = 90^{\circ}$,$\therefore ∠A + ∠DEC = 90^{\circ}$
$\therefore ∠EFA = 90^{\circ}$。$\therefore EF⊥AB$。
9. 对于多项式$x^{2}+2ax+a^{2}$可以直接用公式法分解为$(x+a)^{2}$的形式,但对于多项式$x^{2}+2ax-3a^{2}$,就不能直接用公式法了,我们可以根据多项式的特点,在$x^{2}+2ax-3a^{2}$中先加上一项$a^{2}$,再减去$a^{2}$这项,使整个式子的值不变.
解题过程如下:
$x^{2}+2ax-3a^{2}= x^{2}+2ax-3a^{2}+a^{2}-a^{2}$(第一步)
$=x^{2}+2ax+a^{2}-a^{2}-3a^{2}$(第二步)
$=(x+a)^{2}-(2a)^{2}$(第三步)
$=(x+3a)(x-a)$.(第四步)
参照上述材料,回答下列问题:
(1)上述因式分解的过程,从第二步到第三步,用到的因式分解的方法是(
A. 提公因式法
B. 平方差公式法
C. 完全平方公式法
D. 没有因式分解
(2)从第三步到第四步用到的因式分解的方法是____
(3)请你参照上述方法把$m^{2}-6mn+8n^{2}$因式分解.
解题过程如下:
$x^{2}+2ax-3a^{2}= x^{2}+2ax-3a^{2}+a^{2}-a^{2}$(第一步)
$=x^{2}+2ax+a^{2}-a^{2}-3a^{2}$(第二步)
$=(x+a)^{2}-(2a)^{2}$(第三步)
$=(x+3a)(x-a)$.(第四步)
参照上述材料,回答下列问题:
(1)上述因式分解的过程,从第二步到第三步,用到的因式分解的方法是(
C
).A. 提公因式法
B. 平方差公式法
C. 完全平方公式法
D. 没有因式分解
(2)从第三步到第四步用到的因式分解的方法是____
平方差公式法
____.(3)请你参照上述方法把$m^{2}-6mn+8n^{2}$因式分解.
$(m - 2n)(m - 4n)$
答案:
【解析】:1. 从第二步$x^{2}+2ax+a^{2}-a^{2}-3a^{2}$到第三步$(x+a)^{2}-(2a)^{2}$,是把$x^{2}+2ax+a^{2}$利用完全平方公式$(m + n)^2 = m^2 + 2mn + n^2$(这里$m=x$,$n = a$)变形为$(x + a)^{2}$,所以用到的因式分解的方法是完全平方公式法,选C。
2. 从第三步$(x+a)^{2}-(2a)^{2}$到第四步$(x + 3a)(x - a)$,是利用平方差公式$m^2 - n^2=(m + n)(m - n)$(这里$m=x + a$,$n = 2a$)进行因式分解,所以用到的因式分解的方法是平方差公式法。
3. 对于$m^{2}-6mn+8n^{2}$,参照上述方法,先加上一项$n^{2}$,再减去$n^{2}$这项,使整个式子的值不变。则$m^{2}-6mn+8n^{2}=m^{2}-6mn+8n^{2}+n^{2}-n^{2}=m^{2}-6mn + 9n^{2}-n^{2}=(m - 3n)^{2}-n^{2}$,再根据平方差公式$(m - 3n)^{2}-n^{2}=(m - 3n + n)(m - 3n - n)=(m - 2n)(m - 4n)$。
【答案】:1. C 2. 平方差公式法 3. $(m - 2n)(m - 4n)$
2. 从第三步$(x+a)^{2}-(2a)^{2}$到第四步$(x + 3a)(x - a)$,是利用平方差公式$m^2 - n^2=(m + n)(m - n)$(这里$m=x + a$,$n = 2a$)进行因式分解,所以用到的因式分解的方法是平方差公式法。
3. 对于$m^{2}-6mn+8n^{2}$,参照上述方法,先加上一项$n^{2}$,再减去$n^{2}$这项,使整个式子的值不变。则$m^{2}-6mn+8n^{2}=m^{2}-6mn+8n^{2}+n^{2}-n^{2}=m^{2}-6mn + 9n^{2}-n^{2}=(m - 3n)^{2}-n^{2}$,再根据平方差公式$(m - 3n)^{2}-n^{2}=(m - 3n + n)(m - 3n - n)=(m - 2n)(m - 4n)$。
【答案】:1. C 2. 平方差公式法 3. $(m - 2n)(m - 4n)$
查看更多完整答案,请扫码查看


