2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,已知$\triangle ADE与\triangle ABC的相似比为1:2$,则$\triangle ADE与\triangle ABC$的面积比为(
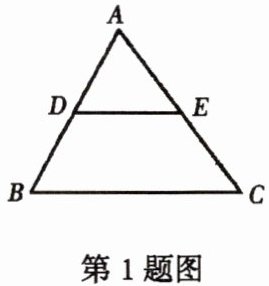
A. $1:2$
B. $1:4$
C. $2:1$
D. $4:1$
B
)
A. $1:2$
B. $1:4$
C. $2:1$
D. $4:1$
答案:
B
2. 如图,在$□ ABCD$中,$AB = 6$,$AD = 9$,$\angle BAD的平分线交BC于点E$,交$DC的延长线于点F$,$BG\perp AE$,垂足为$G$,$BG = 4\sqrt{2}$,则$\triangle CEF$的周长为(
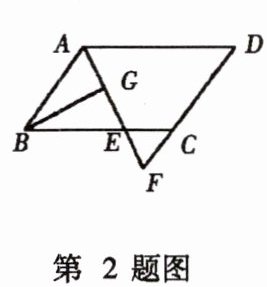
A. $8$
B. $9.5$
C. $10$
D. $11.5$
A
)
A. $8$
B. $9.5$
C. $10$
D. $11.5$
答案:
A
3. 将$a^{3}-2a^{2}+a$分解因式,结果为
$a(a - 1)^2$
.
答案:
$a(a - 1)^2$
4. 化简:$\frac{a + 1}{a - 1}\cdot\frac{a^{2}-1}{a + 1}-1= $
a
.
答案:
a
5. 不等式组$\begin{cases}2x + 5\leqslant 3(x + 2),\frac{x - 1}{2}<\frac{x}{3}\end{cases}$的整数解的个数为
4
.
答案:
4
6. 当$m = $
-6
时,关于$x的分式方程\frac{2x + m}{x - 3}= -1$无解.
答案:
-6
7. 根据条件求值:
(1)已知$\frac{1}{x}+x = 5$,求$\frac{1}{x^{2}}+x^{2}$的值;
(2)已知$4a^{2}+9b^{2}-4a + 12b + 5 = 0$,求$a$
(1)已知$\frac{1}{x}+x = 5$,求$\frac{1}{x^{2}}+x^{2}$的值;
23
(2)已知$4a^{2}+9b^{2}-4a + 12b + 5 = 0$,求$a$
$\frac{1}{2}$
,$b$$-\frac{2}{3}$
的值.
答案:
解:
(1)$\frac{1}{x^2}+x^2=(x+\frac{1}{x})^2 - 2 = 5^2 - 2 = 23$;
(2)$4a^2 + 9b^2 - 4a + 12b + 5$
$= 4a^2 - 4a + 1 + 9b^2 + 12b + 4$
$=(2a - 1)^2 + (3b + 2)^2$
由已知条件有$(2a - 1)^2 + (3a + 2)^2 = 0$,
$\because(2a - 1)^2\geq0$,$(3a + 2)^2\geq0$,
$\therefore 2a - 1 = 0$,$3b + 2 = 0$,即$a = \frac{1}{2}$,$b = -\frac{2}{3}$。
(1)$\frac{1}{x^2}+x^2=(x+\frac{1}{x})^2 - 2 = 5^2 - 2 = 23$;
(2)$4a^2 + 9b^2 - 4a + 12b + 5$
$= 4a^2 - 4a + 1 + 9b^2 + 12b + 4$
$=(2a - 1)^2 + (3b + 2)^2$
由已知条件有$(2a - 1)^2 + (3a + 2)^2 = 0$,
$\because(2a - 1)^2\geq0$,$(3a + 2)^2\geq0$,
$\therefore 2a - 1 = 0$,$3b + 2 = 0$,即$a = \frac{1}{2}$,$b = -\frac{2}{3}$。
查看更多完整答案,请扫码查看


