《2025年新锐图书假期园地暑假作业中原农民出版社八年级数学北师大版》

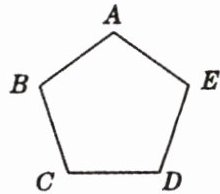
8. 如图所示,甲、乙两人想在正五边形$ABCDE内部找一点P$,使得四边形$ABPE$为平行四边形。其作法如下：(甲)连接$BD$,$CE$,两线段相交于$P$点,则$P$即为所求。(乙)先取$CD的中点M$,再以$A$为圆心,$AB$的长为半径画弧,交$AM于P$点,则$P$即为所求。对于甲、乙两人的作法,正确的是____甲__。

答案： 甲

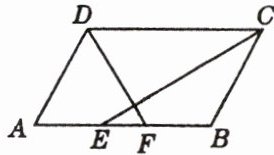
9. 如图所示,在平行四边形$ABCD$中,$CE$,$DF分别是\angle BCD$,$\angle ADC$的平分线,交$AB于E$,$F$,且$AB= 15$,$AD= 8$。求$EF$的长为1。

答案： 【解析】：
- 因为四边形$ABCD$是平行四边形，所以$AB// CD$，$AD = BC = 8$，$AB = CD = 15$。
- 由于$AB// CD$，所以$\angle DFC=\angle FDC$，又因为$DF$是$\angle ADC$的平分线，所以$\angle ADF=\angle FDC$，则$\angle ADF=\angle DFC$，所以$AD = AF = 8$。
- 同理可得$\angle CEB=\angle ECD$，因为$CE$是$\angle BCD$的平分线，所以$\angle BCE=\angle ECD$，则$\angle CEB=\angle BCE$，所以$BC = BE = 8$。
- 那么$AF + BE=8 + 8 = 16$，而$AF + BE=AB + EF$（$AF + BE$中$EF$部分重复计算了一次）。
- 已知$AB = 15$，所以$EF=(AF + BE)-AB=16 - 15 = 1$。
【答案】：$1$

10. 已知：如图所示,$DE为\triangle ABC的边AB$的垂直平分线,$CD为\triangle ABC$的外角平分线,与$DE交于点D$,$DM\perp BC的延长线于点M$,$DN\perp AC于点N$。求证：$AN= BM$。


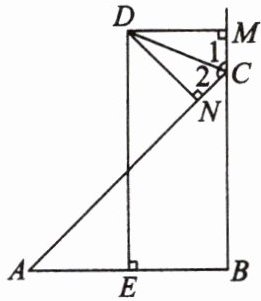
证明：连接AD、BD。
∵DE是AB的垂直平分线，∴AD=BD。
∵CD是△ABC的外角平分线，DM⊥BM，DN⊥AC，∴DM=DN。
在Rt△ADN和Rt△BDM中，$\left\{\begin{array}{l}AD = BD\\DN = DM\end{array}\right.$，∴Rt△ADN≌Rt△BDM(HL)。
∴AN=BM。

答案： 【解析】：
- 连接$AD$、$BD$。
- 因为$DE$是$AB$的垂直平分线，根据垂直平分线的性质：线段垂直平分线上的点到这条线段的两个端点的距离相等，所以$AD = BD$。
- 因为$CD$是$\triangle ABC$的外角平分线，$DM\perp BC$的延长线，$DN\perp AC$，根据角平分线的性质：角平分线上的点到角两边的距离相等，所以$DM = DN$。
- 在$Rt\triangle ADN$和$Rt\triangle BDM$中，$\left\{\begin{array}{l}AD = BD\\DN = DM\end{array}\right.$，根据$HL$（斜边 - 直角边）定理：斜边和一条直角边对应相等的两个直角三角形全等，可得$Rt\triangle ADN\cong Rt\triangle BDM$。
- 再根据全等三角形的性质：全等三角形的对应边相等，所以$AN = BM$。
【答案】：
连接$AD$、$BD$。
$\because DE$是$AB$的垂直平分线，$\therefore AD = BD$。
$\because CD$是$\triangle ABC$的外角平分线，$DM\perp BM$，$DN\perp AC$，$\therefore DM = DN$。
在$Rt\triangle ADN$和$Rt\triangle BDM$中，$\left\{\begin{array}{l}AD = BD\\DN = DM\end{array}\right.$，$\therefore Rt\triangle ADN\cong Rt\triangle BDM(HL)$。
$\therefore AN = BM$。