《2025年七彩假期暑假作业七年级数学》

8. 直角三角形中两个锐角的差为$20^{\circ }$,则两个锐角的度数分别为35度,55度.

答案： 35 55

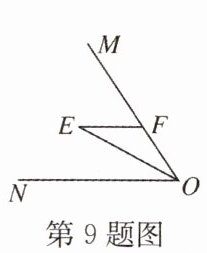
9. 如图,$FE// ON$,OE平分$∠MON,∠FEO= 28^{\circ }$,则$∠MFE= $56度.

答案： 56

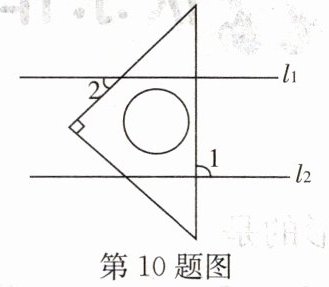
10. 直线$l_{1}// l_{2}$,一块含$45^{\circ }$角的直角三角板如图放置,$∠1= 85^{\circ }$,则$∠2= $$ 40^{\circ} $.

答案： $ 40^{\circ} $

11. 如图,已知$△ABC$,D在BC的延长线上,E在CA的延长线上,F在AB上.试说明：$∠ACD＞∠AFE$.

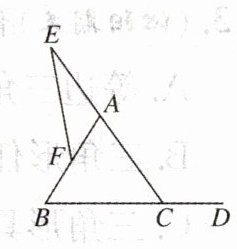
答案： 解：$ \because \angle ACD ＞ \angle BAC $，$ \angle BAC ＞ \angle AFE $，
$ \therefore \angle ACD ＞ \angle AFE $。

12. 如图,BD是$△ABC$的角平分线,$DE// BC$,交AB于点E,$∠A= 45^{\circ },∠BDC= 60^{\circ }$,求$∠BED$的度数.

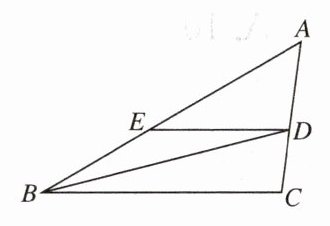
答案： 解：$ \because \angle BDC $ 是 $ \triangle ABD $ 的外角，
$ \therefore \angle ABD = \angle BDC - \angle A = 60^{\circ} - 45^{\circ} = 15^{\circ} $。
$ \because BD $ 是 $ \triangle ABC $ 的角平分线，$ \therefore \angle DBC = \angle ABD = 15^{\circ} $。
$ \because DE // BC $，$ \therefore \angle BDE = \angle DBC = 15^{\circ} $，
$ \therefore \angle BED = 180^{\circ} - \angle BDE - \angle DBE = 180^{\circ} - 15^{\circ} - 15^{\circ} = 150^{\circ} $。

13. 如图所示,$∠ABC= 66^{\circ },∠ACB= 54^{\circ }$,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,求$∠ABE$、$∠ACF和∠BHC$的度数.

答案： 解：$ \because \angle ABC = 66^{\circ} $，$ \angle ACB = 54^{\circ} $，
$ \therefore \angle A = 180^{\circ} - \angle ABC - \angle ACB = 180^{\circ} - 66^{\circ} - 54^{\circ} = 60^{\circ} $。
又 $ \because BE $ 是 $ AC $ 边上的高，所以 $ \angle AEB = 90^{\circ} $，
$ \therefore \angle ABE = 180^{\circ} - \angle BAC - \angle AEB = 180^{\circ} - 60^{\circ} - 90^{\circ} = 30^{\circ} $。
同理，$ \angle ACF = 30^{\circ} $。
$ \therefore \angle BHC = \angle BEC + \angle ACF = 90^{\circ} + 30^{\circ} = 120^{\circ} $。