7. 规定:一个数的平方等于$-1$,记作$i^2= -1$,于是可知$i^3= i^2 × i= (-1) × i$,$i^4= (i^2)^2= (-1)^2= 1$,……$ $按照这样的规律,$i^{2019}$等于()
A. $1$
B. $-1$
C. $i$
D. $-i$
A. $1$
B. $-1$
C. $i$
D. $-i$
答案:
题目中未提供该题答案,跳过
8. 算术平方根等于它本身的实数是______。
答案:
0,1
9. $\frac{4}{9}$的平方根是______;$125$的立方根是______。
答案:
±$\frac{2}{3}$ 5
10. 若$|a|= 5$,$b= -2$,$ab>0$,则$a+b= $______。
答案:
-7
11. 已知实数$x满足x= 2020^2+2021^2$,求代数式$\sqrt{2x-1}$的值等于______。
答案:
4041
12. 在$\frac{\pi}{2}$,$3.14$,$0$,$0.1010010001…$,$\frac{2}{3}$中,无理数有______个。
答案:
2
13. 已知$3x+1的算术平方根是4$,$x+2y的立方根是-1$,
(1)求$x$、$y$的值;
(2)求$2x-5y$的平方根。
(1)求$x$、$y$的值;
(2)求$2x-5y$的平方根。
答案:
(1)根据题意知3x + 1 = 16,x + 2y = -1,则x = 5,y = -3;
(2)
∵2x - 5y = 10 + 15 = 25,
则2x - 5y的平方根为±5。
(1)根据题意知3x + 1 = 16,x + 2y = -1,则x = 5,y = -3;
(2)
∵2x - 5y = 10 + 15 = 25,
则2x - 5y的平方根为±5。
14. 规定:$[m]为不大于m$的最大整数;
(1)填空:$[3.2]= $______,$[-4.8]= $______;
(2)已知动点$C在数轴上表示数a$,且$-2 \leq [a] \leq 4$,则$a$的取值范围是______;
(3)如图,$OB= 1$,$AB \perp OB$,且$AB= 10$,动点$D在数轴上表示的数为t$,设$AD-BD= n$,且$6 \leq [n] \leq 7$,求$t$的取值范围。
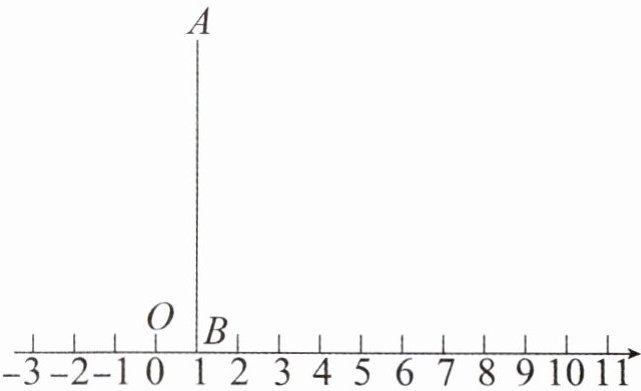
(1)填空:$[3.2]= $______,$[-4.8]= $______;
(2)已知动点$C在数轴上表示数a$,且$-2 \leq [a] \leq 4$,则$a$的取值范围是______;
(3)如图,$OB= 1$,$AB \perp OB$,且$AB= 10$,动点$D在数轴上表示的数为t$,设$AD-BD= n$,且$6 \leq [n] \leq 7$,求$t$的取值范围。

答案:
(1)3 -5
(2) -2 ≤ a < 5
(3)如图,当点D在点B的右边时,

∵6 ≤ [n] ≤ 7,
∴6 ≤ n < 8,
当n = 8时,$\sqrt{(t - 1)^2 + 10^2} - (t - 1) = 8$,
解得t = $\frac{13}{4}$,
当n = 6时,$\sqrt{(t - 1)^2 + 10^2} - (t - 1) = 6$,
解得t = $\frac{19}{3}$,
观察图象可知,$\frac{13}{4}$ < t ≤ $\frac{19}{3}$。
当点D在点B的左边时,同理可得 -$\frac{13}{3}$ < t ≤ -$\frac{5}{4}$,
综上所述,满足条件的t的值为 -$\frac{13}{3}$ ≤ t < -$\frac{5}{4}$ 或 $\frac{13}{4}$ < t ≤ $\frac{19}{3}$。
(1)3 -5
(2) -2 ≤ a < 5
(3)如图,当点D在点B的右边时,

∵6 ≤ [n] ≤ 7,
∴6 ≤ n < 8,
当n = 8时,$\sqrt{(t - 1)^2 + 10^2} - (t - 1) = 8$,
解得t = $\frac{13}{4}$,
当n = 6时,$\sqrt{(t - 1)^2 + 10^2} - (t - 1) = 6$,
解得t = $\frac{19}{3}$,
观察图象可知,$\frac{13}{4}$ < t ≤ $\frac{19}{3}$。
当点D在点B的左边时,同理可得 -$\frac{13}{3}$ < t ≤ -$\frac{5}{4}$,
综上所述,满足条件的t的值为 -$\frac{13}{3}$ ≤ t < -$\frac{5}{4}$ 或 $\frac{13}{4}$ < t ≤ $\frac{19}{3}$。
查看更多完整答案,请扫码查看


