《2025年暑假作业知识出版社七年级理科》

12. 如图,用吸管吸易拉罐内的饮料时,若$∠1= 110^{\circ }$,则$∠2= $______(易拉罐的上、下底面互相平行).

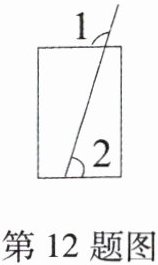
答案： $70^{\circ}$

13. 如图,直线 a,b 被直线 c 所截,且$a// b$. 若$∠1= 118^{\circ }$,求$∠2$的度数.

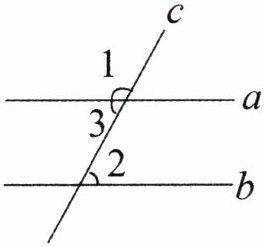
答案： $\because \angle 1+\angle 3=180^{\circ}$（平角的定义），
又$\because \angle 1=118^{\circ}$（已知），
$\therefore \angle 3=180^{\circ}-\angle 1=180^{\circ}-118^{\circ}=62^{\circ}$.
$\because a// b$（已知），
$\therefore \angle 2=\angle 3=62^{\circ}$（两直线平行，内错角相等）.

14. 如图.
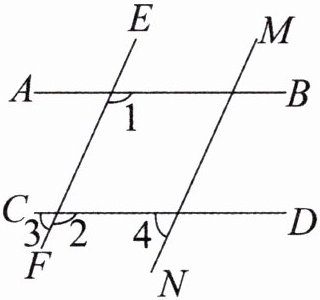
(1)已知$AB// CD,EF// MN,∠1= 115^{\circ }$,求$∠2和∠4$的度数；
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来；
(3)利用(2)的结论解答：如果两个角的两边分别平行,其中一角是另一角的 2 倍,求这两个角的大小.

答案：
(1)$\because AB// CD$，$\angle 1=115^{\circ}$，
$\therefore \angle 2=\angle 1=115^{\circ}$.
$\because EF// MN$，
$\therefore \angle 4=180^{\circ}-\angle 2=180^{\circ}-115^{\circ}=65^{\circ}$.
(2)如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补.
(3)根据
(2)，设其中一个角为$x$，则另一个角为$2x$，有$x+2x=180^{\circ}$，解得$x=60^{\circ}$。
故这两个角的大小分别为$60^{\circ}$，$120^{\circ}$.

15. 如图,$DA⊥AB$,DE 平分$∠ADC$,CE 平分$∠DCB$,且$∠1+∠2= 90^{\circ }$. 试猜想 BC 与 AB 有怎样的位置关系,并说明理由.

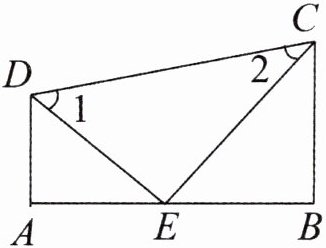
答案： $BC$与$AB$的位置关系是$BC\perp AB$.理由如下：
$\because DE$平分$\angle ADC$，$CE$平分$\angle DCB$（已知），
$\therefore \angle ADC=2\angle 1$，$\angle DCB=2\angle 2$（角平分线定义）.
$\because \angle 1+\angle 2=90^{\circ}$（已知），
$\therefore \angle ADC+\angle DCB=2\angle 1+2\angle 2=2(\angle 1+\angle 2)=2\times 90^{\circ}=180^{\circ}$.
$\therefore AD// BC$（同旁内角互补，两直线平行）.
$\therefore \angle A+\angle B=180^{\circ}$（两直线平行，同旁内角互补）.
$\because DA\perp AB$（已知），
$\therefore \angle A=90^{\circ}$（垂直的定义）.
$\therefore \angle B=180^{\circ}-\angle A=180^{\circ}-90^{\circ}=90^{\circ}$.
$\therefore BC\perp AB$（垂直的定义）.