《2025年暑假作业及活动新疆文化出版社七年级数学》

4. 在平面内画四条直线,使它们分别满足下列条件：
(1)没有交点 (2)有1个交点 (3)有3个交点
(4)有4个交点 (5)有5个交点 (6)有6个交点

答案： 本题可根据直线的位置关系来画出满足条件的图形。
$(1)$ 没有交点
当四条直线相互平行时，它们没有交点。
$(2)$ 有$1$个交点
四条直线相交于同一点时，交点个数为$1$个。
$(3)$ 有$3$个交点
先画三条直线相交于一点，再画第四条直线与其中两条直线平行且与第三条直线相交，此时交点个数为$3$个。
$(4)$ 有$4$个交点
画两组平行线，且这两组平行线相交，此时交点个数为$4$个。
$(5)$ 有$5$个交点
先画三条直线两两相交（不共点），再画第四条直线与其中三条直线相交（不过已有的交点），此时交点个数为$5$个。
$(6)$ 有$6$个交点
四条直线两两相交且任意三条直线不共点时，交点个数为$\frac{4×(4 - 1)}{2}=6$个（根据$n$条直线两两相交且任意三条直线不共点时，交点个数公式$\frac{n(n - 1)}{2}$，$n = 4$代入可得）。
综上，可根据上述分析画出满足条件的图形（由于是画图题，此处省略具体图形，你可根据文字描述自行绘制）。

5. 如图4,写出能使AB//CD的所有可能的条件。

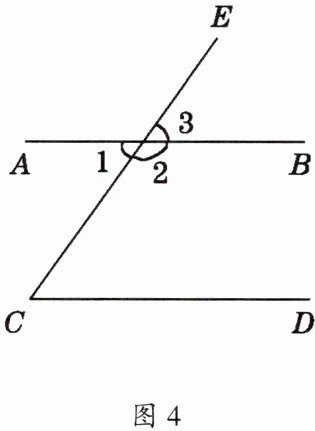
答案： $ \angle 1 = \angle C $ 或 $ \angle 3 = \angle C $ 或 $ \angle 2 + \angle C = 180^\circ $