《2025年暑假作业及活动新疆文化出版社七年级数学》

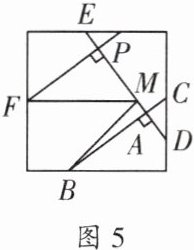
2. 李强同学在王玲同学折纸的基础上,补充了条件：如图5,在线段AP上任取一点M,连接FM、BM,请你猜想∠ABM、∠PFM与∠BMF这三个角之间的数量关系,并说明理由。

答案：
解：如右图所示，过点 $ M $ 作 $ MN// BC $，
$\therefore \angle ABM=\angle BMN$，
$\because PF// BC$，

$\therefore PF// MN$，
$\therefore \angle PFM=\angle FMN$，
$\therefore \angle BMF=\angle BMN+\angle FMN=\angle ABM+\angle PFM$.