第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. 完成下列证明过程:
如图 3,已知$∠B= ∠AEF,EF// AD.$
求证:$AD// BC.$
证明:$\because ∠B= ∠AEF$()
$\therefore EF// BC$()
又$\because EF// AD$()
$AD// BC$()
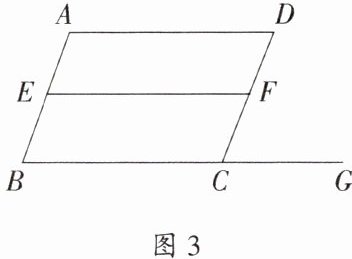
如图 3,已知$∠B= ∠AEF,EF// AD.$
求证:$AD// BC.$
证明:$\because ∠B= ∠AEF$()
$\therefore EF// BC$()
又$\because EF// AD$()
$AD// BC$()

答案:
已知;同位角相等,两直线平行;已知;平行于同一条直线的两条直线平行
2. 如图 4,$AB⊥BC,BC⊥CD,∠1= ∠2.$
求证:$BE// CF.$
证明:$\because AB⊥BC,BC⊥CD$(已知)
$\therefore$ = $=90^{\circ }$()
$\because ∠1= ∠2$(已知)
$\therefore ∠ABC-∠1= ∠BCD-∠2$
即$∠EBC= ∠BCF$
$\therefore$ $//$ ()
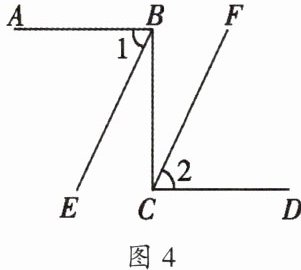
求证:$BE// CF.$
证明:$\because AB⊥BC,BC⊥CD$(已知)
$\therefore$ = $=90^{\circ }$()
$\because ∠1= ∠2$(已知)
$\therefore ∠ABC-∠1= ∠BCD-∠2$
即$∠EBC= ∠BCF$
$\therefore$ $//$ ()

答案:
$ \angle ABC $;$ \angle BCD $;垂直的定义;$ BE $;$ CF $;内错角相等,两直线平行
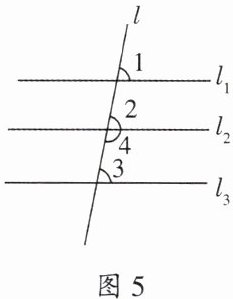
1. 如图 5,在括号内填写依据:
$\because l_{1}// l_{2}$(已知),
$\therefore ∠1= $ (两直线平行,同位角相等)
$\because l_{2}// l_{3}$(已知),
$\therefore ∠3+∠4= $ ()
$\because l_{1}// l_{2}$(已知),
$\therefore ∠1= $ (两直线平行,同位角相等)
$\because l_{2}// l_{3}$(已知),
$\therefore ∠3+∠4= $ ()

答案:
$ \angle 2 $;$ 180 ^ { \circ } $;两直线平行,同旁内角互补
查看更多完整答案,请扫码查看


