《2025年暑假作业及活动新疆文化出版社七年级数学》

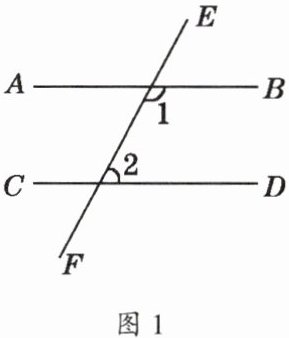
1. 如图 1,$∠1$是它的补角的 5 倍,$∠2的余角是∠2$的 2 倍,那么,$AB// CD$吗？为什么？

答案： $ AB // CD $（提示：$ \angle 1 = 150 ^ { \circ }, \angle 2 = 30 ^ { \circ } $）

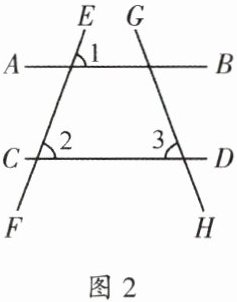
2. 如图 2,$∠3与∠1$互余,$∠3与∠2$互余. 试说明$AB// CD$.

答案： $ \because \angle 3 $与$ \angle 1 $互余，$ \angle 3 $与$ \angle 2 $互余，$ \therefore \angle 3 + \angle 1 = 90 ^ { \circ } $ $ \angle 3 + \angle 2 = 90 ^ { \circ } $
$ \therefore \angle 1 = \angle 2 $（同角的余角相等） $ \therefore AB // CD $（同位角相等，两直线平行）