《2025年春如金卷课时作业AB本八年级数学上册北师大版》

1. 证明命题“若$m＞n$，则$\frac {m}{n}＞1$”是假命题，所举反例正确的是 （B）
A. $m=6$，$n=3$
B. $m=1$，$n=-1$
C. $m=2$，$n=1$
D. $m=0.2$，$n=0.1$

答案： B

2. “等腰三角形的两个底角相等”的逆命题是 （C）
A. 在同一个三角形中，等边对等角
B. 两个角互余的三角形是等腰三角形
C. 如果一个三角形有两个角相等，那么这个三角形是等腰三角形
D. 如果一个三角形有两条边相等，那么这个三角形是等腰三角形

答案： C

3. 对于下列假命题，各举一个反例写在横线上。
（1）“如果$ac=bc$，那么$a=b$”是一个假命题。反例：$a=1$，$b=-1$，$c=0$；
（2）“如果$|a|=|b|$，那么$a=b$”是一个假命题。反例：$a=1$，$b=-1$。

答案： 解：
(1)$a=1$，$b=-1$，$c=0$；
(2)$a=1$，$b=-1$。

4. 把“等角的余角相等”改写成“如果…那么…”的形式，应该是如果两个角是等角的余角，那么它们相等。。

答案： 如果两个角是等角的余角，那么它们相等。

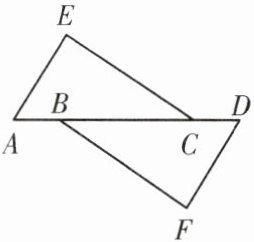
5. 如图，点$A$，$B$，$C$，$D$在同一条直线上，$E$和$F$在直线$AD$两侧，若$∠E=∠F$。请从①$AE=DF$，②$AB=CD$，③$EC// BF$中选两个当条件，第三个当结论构成一个真命题。
（1）条件：②③；（填写序号）
结论：①；（填写序号）
（2）证明你所构建的命题是真命题。

(2)证明：$\because EC// BF$，
$\therefore \angle ACE=\angle DBF$，
$\because AB=CD$，
$\therefore AB+BC=BC+CD$，即$AC=BD$，
在$\triangle ACE$和$\triangle DBF$中，
$\left\{\begin{array}{l} \angle E=\angle F\\ \angle ACE=\angle DBF,\\ AC=BD\end{array}\right.$
$\therefore \triangle ACE≌\triangle DBF(AAS)$，
$\therefore AE=DF$。

答案：
(1)解：条件：②③，结论：①；或条件①③，结论②；
(2)当条件：②③，结论：①时，
证明：$\because EC// BF$，
$\therefore \angle ACE=\angle DBF$，
$\because AB=CD$，
$\therefore AB+BC=BC+CD$，即$AC=BD$，
在$\triangle ACE$和$\triangle DBF$中，
$\left\{\begin{array}{l} \angle E=\angle F\\ \angle ACE=\angle DBF,\\ AC=BD\end{array}\right.$
$\therefore \triangle ACE≌\triangle DBF(AAS)$，
$\therefore AE=DF$；
当条件①③，结论②时，
$\because EC// BF$，
$\therefore \angle ACE=\angle DBF$，
在$\triangle ACE$和$\triangle DBF$中，
$\left\{\begin{array}{l} \angle E=\angle F\\ \angle ACE=\angle DBF,\\ AE=DF\end{array}\right.$
$\therefore \triangle ACE≌\triangle DBF(AAS)$，
$\therefore AC=BD$，
$\therefore AC-BC=BD-BC$，
$\therefore AB=CD$。