《2025年春如金卷课时作业AB本八年级数学上册北师大版》

2. 一次函数$y=kx+b$的图象经过点(0,b)。当$k＞0$时，$y$的值随着$x$值的增大而增大；当$k＜0$时，$y$的值随着$x$值的增大而减小。

答案： (0,b),增大,减小

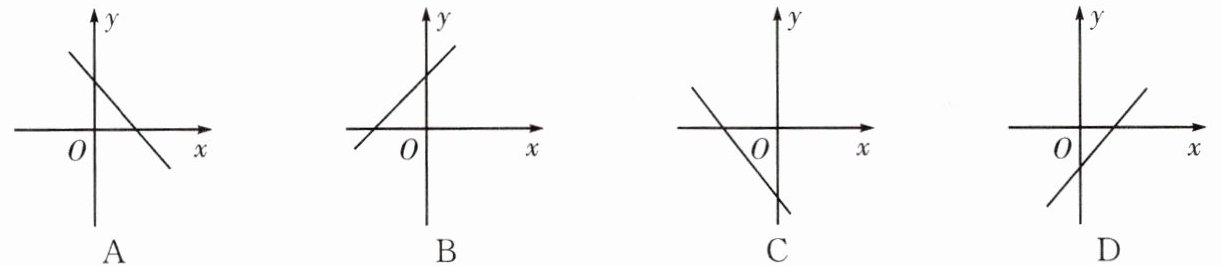
1. 一次函数$y=-\frac{1}{2}x+3$的图象大致是（A）

答案： 1.A

2. 若点$A(x_{1},-1)$，$B(x_{2},1)$，$C(x_{3},5)$都在一次函数$y=-2x-1$的图象上，则$x_{1}$，$x_{2}$，$x_{3}$的大小关系是（C）
A. $x_{1}＜x_{2}＜x_{3}$
B. $x_{1}＜x_{3}＜x_{2}$
C. $x_{3}＜x_{2}＜x_{1}$
D. $x_{2}＜x_{1}＜x_{3}$

答案： 2.C

3. 对于一次函数$y=(3-m)x+1$，函数值$y$随自变量$x$的增大而减小，则$m$的取值范围是$m＞3$。

答案： 3.m＞3

4. 如果直线$y=2x+m$经过点$(1,-3)$，那么$m=$−5。

答案： 4.−5

5. 在平面直角坐标系中，$O$是原点，一次函数$y=-2x+3$与$x$轴交点为$A$，与$y$轴交点为$B$。
（1）写出交点$A$的坐标____，$B$的坐标____；
（2）请直接在平面直角坐标系中，作出一次函数$y=-2x+3$的图象；
（3）求$\triangle AOB$的面积。

答案：
5.解:
(1)当y=0时，−2x+3=0,
　解得:x=$\frac{3}{2}$,
∴点A的坐标为($\frac{3}{2}$,0);
　当x=0时,y=−2×0+3=3,
∴点B的坐标为(0,3)。
故答案为:($\frac{3}{2}$,0),(0,3);
(2)描点、连线，画出函数图象，如图所示;
(3)
∵点A的坐标为($\frac{3}{2}$,0),点B的坐标为(0,3),
∴OA=$\frac{3}{2}$,OB=3,
∴$S_{\triangle AOB}=\frac{1}{2}OA\cdot OB=\frac{1}{2}×\frac{3}{2}×3=\frac{9}{4}$,
∴△AOB的面积为$\frac{9}{4}$。