《2025年春如金卷课时作业AB本八年级数学上册北师大版》

如果三角形的三边长a,b,c满足$a^{2}+b^{2}=c^{2}$，那么这个三角形是直角三角形。

答案： $a^{2}+b^{2}=c^{2}$

1.△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC为直角三角形的是 (B)
A.∠B+∠C=90°
B.∠A:∠B:∠C=3:4:5
C.a=6,b=8,c=10
D.c² - a² = b²

答案： 1. B

2.如图每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为 (B)
A.30°
B.45°
C.50°
D.60°

答案： 2. B

3.下列各组数为勾股数的是④⑤(填序号)。
①1.5,2,3;②3,4,7;③7,12,13;④8,15,17;⑤9,40,41。

答案： 3. ④⑤

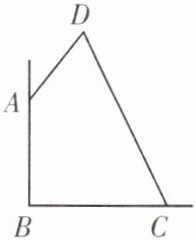
4.为了增强学生体质,丰富校园文化生活,推行中小学生每天锻炼一小时的“阳光体育运动”,某学校决定在校园内某一区域内新建一块塑胶场地,供同学们课间活动使用,如图,已知AB=9m,BC=12m,CD=17m,AD=8m,施工人员在只有卷尺的情况下,通过测量某两点之间的距离,就确定了∠ABC=90°。
(1)请写出施工人员测量的是哪两点之间的距离,以及确定∠ABC=90°的依据;
(2)若平均每平方米的材料成本加施工费为110元,请计算该学校建成这块塑胶场地需花费多少元?

答案：
4. 解：
(1)施工人员测量的是 AC 的距离。
依据：若$AC=15m$，则$∠ABC=90^{\circ }$。
在$\triangle ABC$中，$AB^{2}+BC^{2}=9^{2}+12^{2}=225$，$AC^{2}=15^{2}=225$，
$\therefore AB^{2}+BC^{2}=AC^{2}$，
$\therefore \triangle ABC$为直角三角形，且$∠ABC=90^{\circ }$。
(2)在$\triangle ADC$中，$AD^{2}+AC^{2}=8^{2}+15^{2}=289$，$DC^{2}=17^{2}=289$，
$\therefore \triangle ADC$为直角三角形，且$∠DAC=90^{\circ }$。
$\therefore S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac {1}{2}×9×12+\frac {1}{2}×8×15=114$，
$\therefore 114×110=12540$(元)。