(1)利用平均数、方差进行分析:
$\overline{x}_{A}=$
$S_{A}^{2}=190.17$;$S_{B}^{2}=211.17$;可以看出
(2)利用四分位数、箱线图如下图,进行分析:
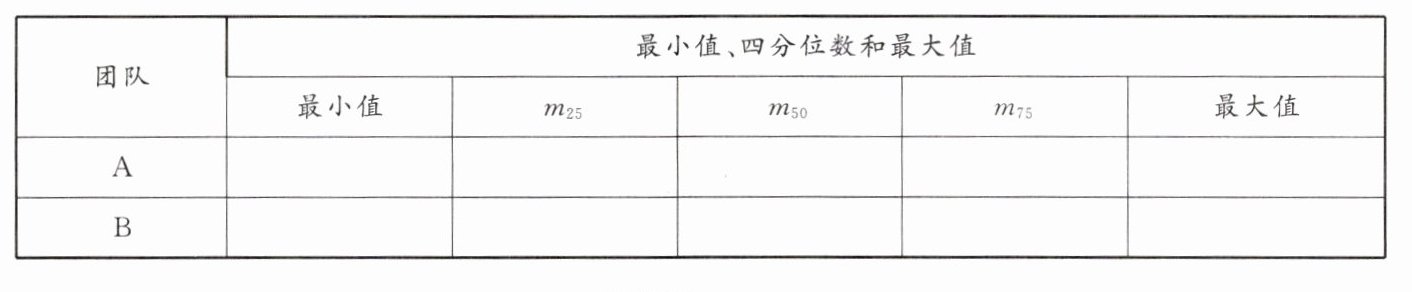
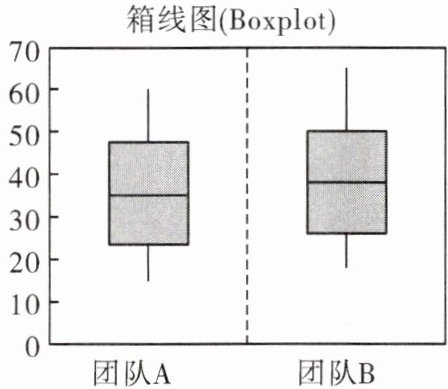
结果分析:
①收益中位数:团队 B(38 万元)高于团队 A(35 万元),表明团队 B 整体收益更高。
②收益稳定性:两队$m_{75}-m_{25}=24$相同(24 万元),波动性一致。
③极端值:两队均无异常值,数据分布较干净。
$\overline{x}_{A}=$
36
;$\overline{x}_{B}=$38
;可以看出B
团队收益较高。$S_{A}^{2}=190.17$;$S_{B}^{2}=211.17$;可以看出
A
团队稳定性较好。(2)利用四分位数、箱线图如下图,进行分析:


结果分析:
①收益中位数:团队 B(38 万元)高于团队 A(35 万元),表明团队 B 整体收益更高。
②收益稳定性:两队$m_{75}-m_{25}=24$相同(24 万元),波动性一致。
③极端值:两队均无异常值,数据分布较干净。
答案:
(1)36 38 B A
(2)
结果分析:①收益中位数:团队 B(38 万元)高于团队 A(35 万元),表明团队 B 整体收益更高。
②收益稳定性:两队$m_{75}-m_{25}=24$相同(24 万元),波动性一致。
③极端值:两队均无异常值,数据分布较干净。
(1)36 38 B A
(2)
结果分析:①收益中位数:团队 B(38 万元)高于团队 A(35 万元),表明团队 B 整体收益更高。
②收益稳定性:两队$m_{75}-m_{25}=24$相同(24 万元),波动性一致。
③极端值:两队均无异常值,数据分布较干净。
查看更多完整答案,请扫码查看


