《2025年春如金卷课时作业AB本八年级数学上册北师大版》

1. 设一次函数的表达式为$y = kx + b(k \neq 0)$，把该一次函数图象上已知点的坐标代入，即可求出$k$，$b$的值。

答案： 已知点

2. 一般地，当一次函数$y = kx + b$的函数值为0时，相应的自变量的值就是方程$kx + b = 0$的解，从图象上看，一次函数$y = kx + b$的图象与$x$轴交点的横坐标就是方程$kx + b = 0$的解。

答案： 0，横坐标

1. 如图，入射光线$MN$经平面镜（$y$轴）上的点$N$反射后，反射光线$NP$交$x$轴于点$P(-1,0)$，若光线$MN$满足的一次函数关系式为$y = ax + \frac{1}{2}$，则$a$的值是（ ）

A. $-\frac{1}{2}$
B. $-\frac{1}{3}$
C. $-\frac{\sqrt{2}}{2}$
D. $-\frac{\sqrt{3}}{3}$

答案：
A 【解析】如图,延长MN交x轴于点$P'$,过点N作$AB⊥y$轴。
根据光的反射定律，$∠MNA = ∠PNA$，
$\because ∠MNA = ∠BNP'$，
$\therefore ∠PNA = ∠BNP'$，
$\because ∠PNA + ∠PNO = 90^{\circ}, ∠BNP' + ∠P'NO = 90^{\circ}$，
$\therefore ∠PNO = ∠P'NO$，
在$Rt△PNO$与$Rt△P'NO$中，
$\left\{\begin{array}{l} ∠PNO = ∠P'NO\\ NO = NO\\ ∠PON = ∠P'ON\end{array}\right. $
$\therefore Rt△PNO ≌ Rt△P'NO(ASA)$，
$\therefore OP = OP'$，
$\because P(-1,0)$，
$\therefore P'(1,0)$，
将$P'(1,0)$代入$y = ax + \frac{1}{2}$，
得$a + \frac{1}{2} = 0$，
解得$a = -\frac{1}{2}$。
故选：A。

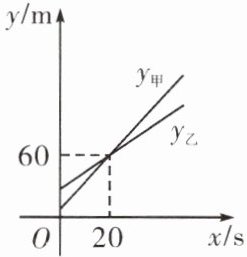
2. 某校科技节上，同学们在操场上进行无人机表演，其中甲、乙两架无人机离操场地面的高度$y$（单位：$m$）与表演时间$x$（单位：$s$）的图象如图所示。已知表演开始时甲、乙离地的高度分别是$5m$，$15m$，在$1min$的表演过程中甲、乙两架无人机的高度差不超过$5m$的时间有____20$s$。

答案： 20 【解析】设$y_{甲} = k_{1}x + b_{1}$，
将$(0,5)$，$(20,60)$分别代入，
即$\left\{\begin{array}{l} 5 = b_{1}\\ 60 = 20k_{1} + b_{1}\end{array}\right. $，
解得：$\left\{\begin{array}{l} k_{1} = 2.75\\ b_{1} = 5\end{array}\right. $，
则$y_{甲} = 2.75x + 5$，
设$y_{乙} = k_{2}x + b_{2}$，
将$(0,15)$，$(20,60)$分别代入，
即$\left\{\begin{array}{l} 15 = b_{2}\\ 60 = 20k_{2} + b_{2}\end{array}\right. $，
解得：$\left\{\begin{array}{l} k_{2} = 2.25\\ b_{2} = 15\end{array}\right. $，
则$y_{乙} = 2.25x + 15$，
当$x ＜ 20$时，$y_{乙} - y_{甲} = 5$，
即$2.25x + 15 - 2.75x - 5 = 5$，
解得：$x = 10$，
当$x ＞ 20$时，$y_{乙} - y_{甲} = -5$，
即$2.25x + 15 - 2.75x - 5 = -5$，
解得：$x = 30$，
$30 - 10 = 20$(秒)，
答：在1分钟的表演过程中甲、乙两架无人机的高度差不超过5米的时间可持续20s。
故答案为：20。

3. 某快递物流总站送货，快递车出发$0.5h$后，物流人员发现遗漏重要快递，于是便驾小车沿相同路线追赶快递车。已知快递车行驶的速度是$60km/h$，小车行驶的速度是$80km/h$。
（1）求小车出发后多少小时追上快递车？
（2）如图，图中$OB$，$AB$分别表示小车、快递车离开物流总站的路程$y(km)$与小车行驶的时间$x(h)$的函数关系的图象。试求$AB$所在直线的解析式；
（3）假设小车需要在$1h$内追上快递车，因此出发追赶时通知快递车减速匀速行驶，求快递车至少减速至多少，小车才能在$1h$内追上？

答案： 解：
(1)设小车行驶的时间为$x h$，则快递车行驶的时间为$(x + 0.5)h$，
根据题意，得$80x = 60(x + 0.5)$，
解得$x = 1.5$，
$\therefore$小车出发后1.5h追上快递车；
(2)$\because$小车出发后1.5h追上快递车，与物流总站相距120km，
$\therefore$点B的坐标是$(1.5,120)$，
由题意，得点A的坐标为$(0,30)$，
设直线AB的解析式为$y = kx + b$，
将$A(0,30)$，$B(1.5,120)$代入，得：
$\left\{\begin{array}{l} b = 30\\ 1.5k + b = 120\end{array}\right. $，
解得$\left\{\begin{array}{l} k = 60\\ b = 30\end{array}\right. $，
$\therefore AB$所在直线的解析式为$y = 60x + 30$；
(3)设快递车速度减速至$v km/h$，
则$80×1 ≥ 30 + v$，
解得$v ≤ 50$，
$\therefore$快递车至少减速至50km/h。