勾股定理:直角三角形两直角边的平方和等于斜边的平方。如果用a,b和c分别表示直角三角形的两条直角边长和斜边长,那么
$a^{2}+b^{2}=c^{2}$
。
答案:
$a^{2}+b^{2}=c^{2}$
1. 如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形面积为 (
A. 194
B. 144
C. 14
D. 12
B
)A. 194
B. 144
C. 14
D. 12
答案:
1. B
2. 轩轩同学在校园里散步时看到鸟儿飞来飞去的场景,提出了一个有趣的数学问题:有两棵树,一棵高6m,另一棵高2m,两树相距6m,一只小鸟要从一棵树的树顶到另一棵树的树顶,至少需要飞多远? 下列结果最接近的是 (
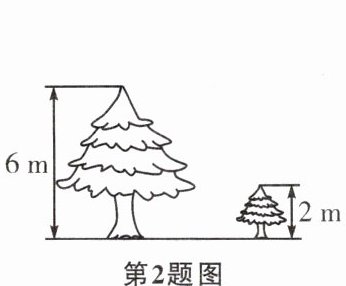
A. 5m
B. 6m
C. 7m
D. 8m
C
)
A. 5m
B. 6m
C. 7m
D. 8m
答案:
2. C
3. 我国古代数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”,如图所示,它是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,若大正方形的面积是52,每个直角三角形的长直角边与短直角边的比是3:2,则小正方形的面积为
4
。
答案:
3. 4
4. 用四个全等的直角三角形拼成如图1所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a < b),斜边长为c。
(1)请利用图1证明:$a^{2}+b^{2}=c^{2}$;
(2)如图2,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积。
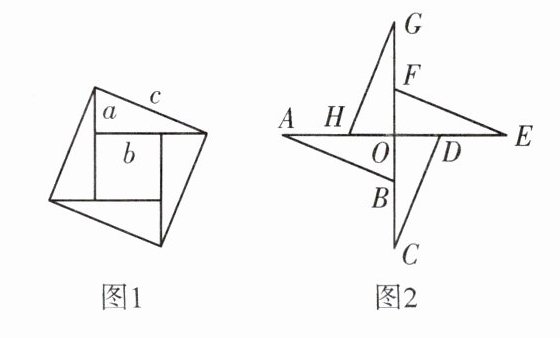
(1)请利用图1证明:$a^{2}+b^{2}=c^{2}$;
(2)如图2,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积。

答案:
4.
(1)证明:$S_{小正方形}=(b-a)^{2}=a^{2}-2ab+b^{2}$,
$S_{小正方形}=c^{2}-4×\frac {1}{2}ab=c^{2}-2ab$,
即$b^{2}-2ab+a^{2}=c^{2}-2ab$,
$\therefore a^{2}+b^{2}=c^{2}$;
(2)解:$\because AB+BC=80÷4=20$,
设$AH=BC=x$,则$AB=20-x$,$OH=OB=5$,
在$Rt\triangle AOB$中,由勾股定理得:
$OH^{2}+OG^{2}=GH^{2}$,
即$5^{2}+(5+x)^{2}=(20-x)^{2}$,
解得:$x=7$,
$\therefore S=\frac {1}{2}×5×12×4=120$。
(1)证明:$S_{小正方形}=(b-a)^{2}=a^{2}-2ab+b^{2}$,
$S_{小正方形}=c^{2}-4×\frac {1}{2}ab=c^{2}-2ab$,
即$b^{2}-2ab+a^{2}=c^{2}-2ab$,
$\therefore a^{2}+b^{2}=c^{2}$;
(2)解:$\because AB+BC=80÷4=20$,
设$AH=BC=x$,则$AB=20-x$,$OH=OB=5$,
在$Rt\triangle AOB$中,由勾股定理得:
$OH^{2}+OG^{2}=GH^{2}$,
即$5^{2}+(5+x)^{2}=(20-x)^{2}$,
解得:$x=7$,
$\therefore S=\frac {1}{2}×5×12×4=120$。
查看更多完整答案,请扫码查看


