4. 亮点原创 (6分)2024年11月12日,第十五届珠海航展上我国新型隐身战机歼-35A首次进行公开飞行表演,展示其优异的机动性能.表演过程中,歼-35A发动机尾喷管喷出一串漂亮的马赫环(如图所示)后垂直冲进云里.歼-35A采用了双发设计,每台发动机的推力约为90千牛,作战半径约1 350千米.其油箱设计精巧,能够容纳总计8.5吨的燃油,为远程任务提供了坚实的能源保障.燃料使用航空煤油,航空煤油具有较高的热值和出色的燃烧效率,热值一般为45 MJ/kg.求:
(1)若该机以最大推力飞行一个作战半径,发动机做的功.
(2)若发动机效率达到60%,油量还剩20%时,剩余燃油可供歼-35A飞行的距离.

(1)若该机以最大推力飞行一个作战半径,发动机做的功.
(2)若发动机效率达到60%,油量还剩20%时,剩余燃油可供歼-35A飞行的距离.

答案:
(1) $ 2.43 \times 10^{11} \, \text{J} $
(2) $ 255 \, \text{km} $ 解析:
(1) 每台发动机推力 90 千牛, 双发动机推力 $ F = 2 \times 90 \times 10^{3} \, \text{N} = 1.8 \times 10^{5} \, \text{N} $, 飞行一个作战半径做的功 $ W = Fs = 1.8 \times 10^{5} \, \text{N} \times 1350 \times 10^{3} \, \text{m} = 2.43 \times 10^{11} \, \text{J} $.
(2) 油量还剩 $ 20\% $ 时, 剩余航空煤油的质量 $ m = 20\% \times 8.5 \, \text{t} = 1.7 \, \text{t} = 1.7 \times 10^{3} \, \text{kg} $, 这些航空煤油完全燃烧放出的热量 $ Q_{\text{放}} = mq = 1.7 \times 10^{3} \, \text{kg} \times 45 \times 10^{6} \, \text{J/kg} = 7.65 \times 10^{10} \, \text{J} $, 可供歼 - 35A 飞行的距离 $ s' = \frac{W'}{F} = \frac{\eta Q_{\text{放}}}{F} = \frac{60\% \times 7.65 \times 10^{10} \, \text{J}}{1.8 \times 10^{5} \, \text{N}} = 2.55 \times 10^{5} \, \text{m} = 255 \, \text{km} $.
(1) $ 2.43 \times 10^{11} \, \text{J} $
(2) $ 255 \, \text{km} $ 解析:
(1) 每台发动机推力 90 千牛, 双发动机推力 $ F = 2 \times 90 \times 10^{3} \, \text{N} = 1.8 \times 10^{5} \, \text{N} $, 飞行一个作战半径做的功 $ W = Fs = 1.8 \times 10^{5} \, \text{N} \times 1350 \times 10^{3} \, \text{m} = 2.43 \times 10^{11} \, \text{J} $.
(2) 油量还剩 $ 20\% $ 时, 剩余航空煤油的质量 $ m = 20\% \times 8.5 \, \text{t} = 1.7 \, \text{t} = 1.7 \times 10^{3} \, \text{kg} $, 这些航空煤油完全燃烧放出的热量 $ Q_{\text{放}} = mq = 1.7 \times 10^{3} \, \text{kg} \times 45 \times 10^{6} \, \text{J/kg} = 7.65 \times 10^{10} \, \text{J} $, 可供歼 - 35A 飞行的距离 $ s' = \frac{W'}{F} = \frac{\eta Q_{\text{放}}}{F} = \frac{60\% \times 7.65 \times 10^{10} \, \text{J}}{1.8 \times 10^{5} \, \text{N}} = 2.55 \times 10^{5} \, \text{m} = 255 \, \text{km} $.
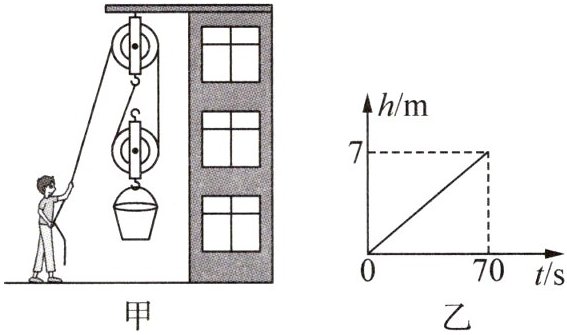
5. (2025·江苏宿迁期中·8分)生活中有些低层建筑没有电梯,房屋装修时工人师傅常用滑轮组提升重物.某工人用如图甲所示的滑轮组将400 N的重物匀速提升7 m,拉力$F= 250N$,重物上升的高度h与所用时间t的关系图像如图乙所示.已知工人的质量为50 kg,不计绳重和摩擦,g取10 N/kg.试求:
(1)绳子自由端移动的距离.
(2)在匀速提升重物的过程中,工人拉绳子的功率.
(3)设绳子的承重足够大,该工人使用此滑轮组提升重物时的最高机械效率.
(1)绳子自由端移动的距离.
(2)在匀速提升重物的过程中,工人拉绳子的功率.
(3)设绳子的承重足够大,该工人使用此滑轮组提升重物时的最高机械效率.

答案:
(1) $ 14 \, \text{m} $
(2) $ 50 \, \text{W} $
(3) $ 90\% $ 解析:
(1) 由图甲可知, $ n = 2 $, 重物上升的高度为 $ 7 \, \text{m} $, 则绳子自由端移动的距离 $ s = nh = 2 \times 7 \, \text{m} = 14 \, \text{m} $.
(2) 由图乙可知, 将重物匀速提升 $ 7 \, \text{m} $ 所用的时间 $ t = 70 \, \text{s} $, 则在匀速提升重物的过程中, 工人拉绳子的功率 $ P = \frac{W}{t} = \frac{Fs}{t} = \frac{250 \, \text{N} \times 14 \, \text{m}}{70 \, \text{s}} = 50 \, \text{W} $.
(3) 机械效率 $ \eta = \frac{W_{\text{有用}}}{W_{\text{总}}} \times 100\% = \frac{G_{\text{物}} h}{G_{\text{物}} h + G_{\text{动}} h} \times 100\% = \frac{G_{\text{物}}}{G_{\text{物}} + G_{\text{动}}} \times 100\% $, 可知使用同一滑轮组, 提升物体的重力越大, 机械效率越高. 重物的重力为 $ 400 \, \text{N} $ 时, 拉力为 $ 250 \, \text{N} $, 不计绳重和摩擦, 则 $ F = \frac{1}{n} (G_{\text{物}} + G_{\text{动}}) $, 则动滑轮的重力 $ G_{\text{动}} = nF - G_{\text{物}} = 2 \times 250 \, \text{N} - 400 \, \text{N} = 100 \, \text{N} $, 工人的质量为 $ 50 \, \text{kg} $, 则工人能提供的最大拉力 $ F_{\text{max}} = G_{\text{工人}} = m_{\text{工人}} g = 50 \, \text{kg} \times 10 \, \text{N/kg} = 500 \, \text{N} $, 由 $ F = \frac{1}{n} (G_{\text{物}} + G_{\text{动}}) $ 可知, 工人能提升重物的最大重力 $ G_{\text{物 max}} = nF_{\text{max}} - G_{\text{动}} = 2 \times 500 \, \text{N} - 100 \, \text{N} = 900 \, \text{N} $, 则最高机械效率 $ \eta = \frac{W_{\text{有用}}}{W_{\text{总}}} \times 100\% = \frac{G_{\text{物 max}}}{G_{\text{物 max}} + G_{\text{动}}} \times 100\% = \frac{900 \, \text{N}}{900 \, \text{N} + 100 \, \text{N}} \times 100\% = 90\% $.
(1) $ 14 \, \text{m} $
(2) $ 50 \, \text{W} $
(3) $ 90\% $ 解析:
(1) 由图甲可知, $ n = 2 $, 重物上升的高度为 $ 7 \, \text{m} $, 则绳子自由端移动的距离 $ s = nh = 2 \times 7 \, \text{m} = 14 \, \text{m} $.
(2) 由图乙可知, 将重物匀速提升 $ 7 \, \text{m} $ 所用的时间 $ t = 70 \, \text{s} $, 则在匀速提升重物的过程中, 工人拉绳子的功率 $ P = \frac{W}{t} = \frac{Fs}{t} = \frac{250 \, \text{N} \times 14 \, \text{m}}{70 \, \text{s}} = 50 \, \text{W} $.
(3) 机械效率 $ \eta = \frac{W_{\text{有用}}}{W_{\text{总}}} \times 100\% = \frac{G_{\text{物}} h}{G_{\text{物}} h + G_{\text{动}} h} \times 100\% = \frac{G_{\text{物}}}{G_{\text{物}} + G_{\text{动}}} \times 100\% $, 可知使用同一滑轮组, 提升物体的重力越大, 机械效率越高. 重物的重力为 $ 400 \, \text{N} $ 时, 拉力为 $ 250 \, \text{N} $, 不计绳重和摩擦, 则 $ F = \frac{1}{n} (G_{\text{物}} + G_{\text{动}}) $, 则动滑轮的重力 $ G_{\text{动}} = nF - G_{\text{物}} = 2 \times 250 \, \text{N} - 400 \, \text{N} = 100 \, \text{N} $, 工人的质量为 $ 50 \, \text{kg} $, 则工人能提供的最大拉力 $ F_{\text{max}} = G_{\text{工人}} = m_{\text{工人}} g = 50 \, \text{kg} \times 10 \, \text{N/kg} = 500 \, \text{N} $, 由 $ F = \frac{1}{n} (G_{\text{物}} + G_{\text{动}}) $ 可知, 工人能提升重物的最大重力 $ G_{\text{物 max}} = nF_{\text{max}} - G_{\text{动}} = 2 \times 500 \, \text{N} - 100 \, \text{N} = 900 \, \text{N} $, 则最高机械效率 $ \eta = \frac{W_{\text{有用}}}{W_{\text{总}}} \times 100\% = \frac{G_{\text{物 max}}}{G_{\text{物 max}} + G_{\text{动}}} \times 100\% = \frac{900 \, \text{N}}{900 \, \text{N} + 100 \, \text{N}} \times 100\% = 90\% $.
查看更多完整答案,请扫码查看


