《2025年名师测控九年级数学上册人教版》

1. 若二次函数$y = ax^{2}-2ax + c$的图象经过点$(-1,0)$,则方程$ax^{2}-2ax + c = 0$的解为 (C)
A. $x_{1}=-3,x_{2}=-1$
B. $x_{1}=1,x_{2}=3$
C. $x_{1}=-1,x_{2}=3$
D. $x_{1}=-3,x_{2}=1$

答案： C

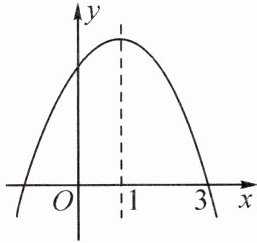
2. 已知二次函数$y = ax^{2}+bx + c(a\neq0)$的图象如图所示,当$y＞0$时,$x$的取值范围是 (D)

A. $-1＜x＜2$
B. $x＞2$
C. $x＜-1$
D. $x＜-1$或$x＞2$

答案： D

3. 若抛物线$y = x^{2}+4x + 5 - m$与$x$轴有两个不同的交点,则$m$的取值范围是 (D)
A. $m＜-1$
B. $0＜m\leqslant1$
C. $m＜1$
D. $m＞1$

答案： D

4. 对于二次函数$y = -\frac{1}{4}x^{2}+x - 4$,下列说法正确的是 (B)
A. 当$x＞0$时,$y$随$x$的增大而增大
B. 当$x = 2$时,$y$有最大值$-3$
C. 图象的对称轴是直线$x = -2$
D. 图象与$x$轴有两个交点

答案： B

5. 已知二次函数$y = ax^{2}+bx + c(a\neq0)$图象的一部分如图所示,点$(-2,0)$在该函数图象上,其对称轴为直线$x = -\frac{1}{2}$,则当$y＞0$时,自变量$x$的取值范围是 (D)

A. $-2＜x＜0$
B. $x＜-2$或$x＞1$
C. $x＜1$
D. $-2＜x＜1$

答案： D

6. 某大学生利用课余时间在网上销售一种成本为50元/件的商品,每月的销售量$y$(件)与销售单价$x$(元/件)之间的函数关系式为$y = -4x + 440$,要获得最大利润,该商品的售价应定为 (C)
A. 60元
B. 70元
C. 80元
D. 90元

答案： C

7. 日渐强大的祖国给了我们安静祥和的学习环境.我国某集团军在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度$y$(m)与飞行时间$x$(s)之间的关系式为$y = -\frac{1}{5}x^{2}+10x$,一枚炮弹从发射到落地,经过的时间为 (C)
A. 10 s
B. 25 s
C. 50 s
D. 100 s

答案： C

8. 如图,已知抛物线$y = ax^{2}+bx + c$的对称轴为直线$x = 1$.给出下列结论:①$ac＜0$;②$b^{2}-4ac＞0$;③$2a - b = 0$;④$a - b + c = 0$.其中,正确的结论有 (C)

A. 1个
B. 2个
C. 3个
D. 4个

答案： C

9. 若二次函数$y = x^{2}-x + a + 1$的图象过原点,则$a$的值为______-1.

答案： $-1$

10. 抛物线$y = ax^{2}$与直线$y = bx + c$的两个交点坐标分别为$A(-2,4)$,$B(1,1)$,则方程$ax^{2}=bx + c$的解是$x_{1}=-2,x_{2}=1$.

答案： $x_{1}=-2,x_{2}=1$

11. 如图,若被击打的小球飞行高度$h$(m)与飞行时间$t$(s)之间具有的关系为$h = 20t - 5t^{2}$,则小球从飞出到落地所用的时间为4s.

答案： 4