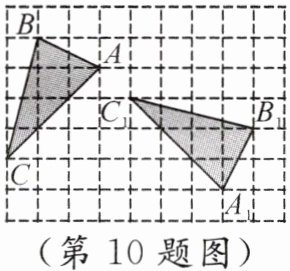
10. 如图,在正方形网格中,格点三角形$ABC$绕某点顺时针旋转角$\alpha(0^{\circ}<\alpha<180^{\circ})$得到格点三角形$A_{1}B_{1}C_{1}$,点$A$与点$A_{1}$,点$B$与点$B_{1}$,点$C$与点$C_{1}$是对应点,则$\alpha=$
$90^{\circ}$
.
答案:
$90^{\circ}$
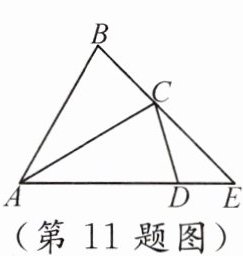
11. 如图,在$△ABC$中,$AB=AC=4$,将$△ABC$绕点$A$顺时针旋转$30^{\circ}$,得到$△ACD$,延长$AD$交$BC$的延长线于点$E$,则$DE$的长为______
$2\sqrt{3}-2$
.
答案:
$2\sqrt{3}-2$
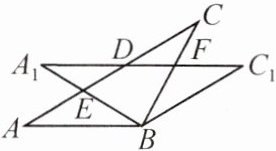
12. 如图,在$△ABC$中,$AB=BC$,将$△ABC$绕点$B$顺时针旋转角$\alpha$,得到$△A_{1}BC_{1}$,$A_{1}B$交$AC$于点$E$,$A_{1}C_{1}$分别交$AC$,$BC$于点$D$,$F$.下列结论:$①∠CDF=\alpha$;$②A_{1}E=CF$;$③DF=FC$;$④AD=CE$;$⑤A_{1}F=CE$.其中,正确的是______
①②⑤
.(填序号)
答案:
①②⑤
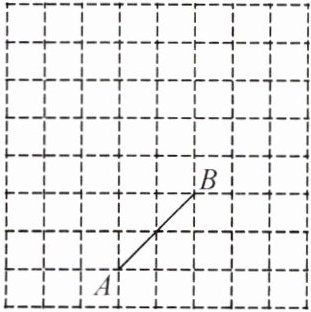
13. (7分)如图,方格纸上每个小正方形的边长均为$1$个单位长度,点$A,B$都在格点上.(两条网格线的交点叫格点)
(1)将线段$AB$向上平移$2$个单位长度,点$A$的对应点为点$A_{1}$,点$B$的对应点为点$B_{1}$,请画出平移后的线段$A_{1}B_{1}$;
(2)将线段$A_{1}B_{1}$绕点$A_{1}$按逆时针方向旋转$90^{\circ}$,点$B_{1}$的对应点为点$B_{2}$,请画出旋转后的线段$A_{1}B_{2}$;
(3)连接$AB_{2},BB_{2}$,求$△ABB_{2}$的面积.
(1)将线段$AB$向上平移$2$个单位长度,点$A$的对应点为点$A_{1}$,点$B$的对应点为点$B_{1}$,请画出平移后的线段$A_{1}B_{1}$;
(2)将线段$A_{1}B_{1}$绕点$A_{1}$按逆时针方向旋转$90^{\circ}$,点$B_{1}$的对应点为点$B_{2}$,请画出旋转后的线段$A_{1}B_{2}$;
(3)连接$AB_{2},BB_{2}$,求$△ABB_{2}$的面积.

答案:
解:
(1) 线段 $A_1B_1$ 如图;
(2) 线段 $A_1B_2$ 如图;
(3) 连接 $AB_2$,$BB_2$ 如图,$S_{\triangle ABB_2}=4\times4 - \frac{1}{2}\times2\times2 - \frac{1}{2}\times2\times4 - \frac{1}{2}\times2\times4=16 - 2 - 4 - 4 = 6$.
解:
(1) 线段 $A_1B_1$ 如图;
(2) 线段 $A_1B_2$ 如图;
(3) 连接 $AB_2$,$BB_2$ 如图,$S_{\triangle ABB_2}=4\times4 - \frac{1}{2}\times2\times2 - \frac{1}{2}\times2\times4 - \frac{1}{2}\times2\times4=16 - 2 - 4 - 4 = 6$.

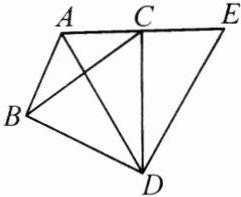
14. (7分)如图,在$△ABC$中,$∠BAC=120^{\circ}$,以$BC$为边向外作等边三角形$BCD$,把$△ABD$绕着点$D$按顺时针方向旋转$60^{\circ}$到$△ECD$的位置(点$A,C,E$三点共线).若$AB=3,AC=2$,求$∠BAD$的度数和$AD$的长.

答案:
解: 由 $ \triangle ABD $ 绕点 $D$ 按顺时针方向旋转 $60^{\circ}$ 得到 $ \triangle ECD $,可得 $AB = CE = 3$,$AD = ED$,$\angle ADE = 60^{\circ}$,$\therefore \triangle ADE$ 为等边三角形,$\therefore \angle DAE = 60^{\circ}$,$\therefore \angle BAD = \angle BAC - \angle DAE = 120^{\circ} - 60^{\circ} = 60^{\circ}$,$AD = AE = AC + CE = 2 + 3 = 5$.
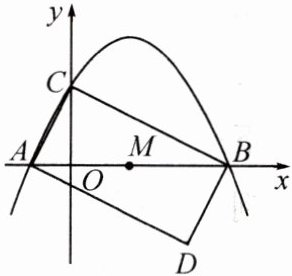
15. (10分)如图,抛物线$y=-\frac{1}{2}x^{2}+\frac{3}{2}x+2$与$x$轴交于点$A,B$,与$y$轴交于点$C$.
(1)写出点$A,B,C$的坐标;
(2)将$△ABC$绕$AB$的中点$M$旋转$180^{\circ}$,得到$△BAD$.
①求点$D$的坐标;
②判断四边形$ADBC$的形状,并说明理由.
(1)写出点$A,B,C$的坐标;
(2)将$△ABC$绕$AB$的中点$M$旋转$180^{\circ}$,得到$△BAD$.
①求点$D$的坐标;
②判断四边形$ADBC$的形状,并说明理由.

答案:
解:
(1) $A(-1,0)$,$B(4,0)$,$C(0,2)$;
(2) ① 连接 $CD$,则 $CD$ 必过点 $M$. 过点 $D$ 作 $DG \perp x$ 轴于点 $G$,易证 $ \triangle COM \cong \triangle DGM$,$\therefore OC = DG = 2$. $ \because M$ 是 $AB$ 的中点,$AB = 4 - (-1) = 5$,$\therefore AM = \frac{5}{2}$,$\therefore OM = \frac{5}{2} - 1 = \frac{3}{2}$,$\therefore M(\frac{3}{2},0)$,$\therefore D(3,-2)$; ② 四边形 $ADBC$ 是矩形. 理由如下: 由旋转的性质,知 $CM = MD$. 又 $ \because AM = BM$,$\therefore$ 四边形 $ADBC$ 是平行四边形. 又 $ \because AC^2 = 1^2 + 2^2 = 5$,$BC^2 = 2^2 + 4^2 = 20$,$AB^2 = 5^2 = 25$,$\therefore AC^2 + BC^2 = AB^2$,$\therefore \angle ACB = 90^{\circ}$,$\therefore$ 四边形 $ADBC$ 是矩形.
(1) $A(-1,0)$,$B(4,0)$,$C(0,2)$;
(2) ① 连接 $CD$,则 $CD$ 必过点 $M$. 过点 $D$ 作 $DG \perp x$ 轴于点 $G$,易证 $ \triangle COM \cong \triangle DGM$,$\therefore OC = DG = 2$. $ \because M$ 是 $AB$ 的中点,$AB = 4 - (-1) = 5$,$\therefore AM = \frac{5}{2}$,$\therefore OM = \frac{5}{2} - 1 = \frac{3}{2}$,$\therefore M(\frac{3}{2},0)$,$\therefore D(3,-2)$; ② 四边形 $ADBC$ 是矩形. 理由如下: 由旋转的性质,知 $CM = MD$. 又 $ \because AM = BM$,$\therefore$ 四边形 $ADBC$ 是平行四边形. 又 $ \because AC^2 = 1^2 + 2^2 = 5$,$BC^2 = 2^2 + 4^2 = 20$,$AB^2 = 5^2 = 25$,$\therefore AC^2 + BC^2 = AB^2$,$\therefore \angle ACB = 90^{\circ}$,$\therefore$ 四边形 $ADBC$ 是矩形.
查看更多完整答案,请扫码查看


