12. 如图,点A到直线l的距离为3,$\odot A$的半径为2,C,P分别为$\odot A$和l上的动点,以PC为直角边的$Rt△PBC$与$\odot A$始终相切于点C,且$∠P=30^{\circ }$,则斜边PB的最小值为
$ \frac { 2 \sqrt { 15 } } { 3 } $
.
答案:
$ \frac { 2 \sqrt { 15 } } { 3 } $
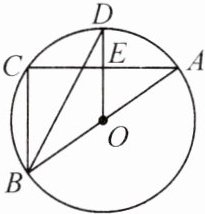
13. (8分)如图,$\odot O$是$△ABC$的外接圆,AB是$\odot O$的直径,半径$OD⊥AC$,垂足为点E,连接BD.
(1)求证:BD平分$∠ABC$;
(2)若$AC=8,DE=2$,求线段BD的长.
(1)求证:BD平分$∠ABC$;
(2)若$AC=8,DE=2$,求线段BD的长.

答案:
解:
(1) $ \because $ 半径 $ O D \perp A C $, $ \therefore \widehat { A D } = \widehat { C D } $, $ \therefore \angle A B D = \angle C B D $, $ \therefore B D $ 平分 $ \angle A B C $;
(2) 过点 $ D $ 作 $ D F \perp B C $, 交 $ B C $ 的延长线于点 $ F $, 则 $ \angle F = 90 ^ { \circ } $. $ \because O D \perp A C $, $ O D $ 是 $ \odot O $ 的半径, $ \therefore C E = A E = \frac { 1 } { 2 } A C = 4 $. $ \because A B $ 是 $ \odot O $ 的直径, $ \therefore \angle A C B = 90 ^ { \circ } $, $ \therefore \angle E C F = 180 ^ { \circ } - \angle A C B = 90 ^ { \circ } $. $ \because O D \perp A C $, $ \therefore \angle C E D = 90 ^ { \circ } $, $ \therefore $ 四边形 $ C E D F $ 是矩形, $ \therefore D F = C E = 4 $, $ C F = D E = 2 $. 设 $ O D = O A = r $, 则 $ O E = r - 2 $. 在 $ \mathrm { Rt } \triangle A E O $ 中, 由勾股定理, 得 $ A E ^ { 2 } + O E ^ { 2 } = O A ^ { 2 } $, 即 $ 4 ^ { 2 } + ( r - 2 ) ^ { 2 } = r ^ { 2 } $, 解得 $ r = 5 $. $ \therefore A B = 2 r = 10 $. 在 $ \mathrm { Rt } \triangle A C B $ 中, 由勾股定理, 得 $ B C = \sqrt { A B ^ { 2 } - A C ^ { 2 } } = \sqrt { 10 ^ { 2 } - 8 ^ { 2 } } = 6 $, $ \therefore B F = B C + C F = 8 $. 在 $ \mathrm { Rt } \triangle B F D $ 中, 由勾股定理, 得 $ B D = \sqrt { B F ^ { 2 } + D F ^ { 2 } } = \sqrt { 8 ^ { 2 } + 4 ^ { 2 } } = 4 \sqrt { 5 } $.
(1) $ \because $ 半径 $ O D \perp A C $, $ \therefore \widehat { A D } = \widehat { C D } $, $ \therefore \angle A B D = \angle C B D $, $ \therefore B D $ 平分 $ \angle A B C $;
(2) 过点 $ D $ 作 $ D F \perp B C $, 交 $ B C $ 的延长线于点 $ F $, 则 $ \angle F = 90 ^ { \circ } $. $ \because O D \perp A C $, $ O D $ 是 $ \odot O $ 的半径, $ \therefore C E = A E = \frac { 1 } { 2 } A C = 4 $. $ \because A B $ 是 $ \odot O $ 的直径, $ \therefore \angle A C B = 90 ^ { \circ } $, $ \therefore \angle E C F = 180 ^ { \circ } - \angle A C B = 90 ^ { \circ } $. $ \because O D \perp A C $, $ \therefore \angle C E D = 90 ^ { \circ } $, $ \therefore $ 四边形 $ C E D F $ 是矩形, $ \therefore D F = C E = 4 $, $ C F = D E = 2 $. 设 $ O D = O A = r $, 则 $ O E = r - 2 $. 在 $ \mathrm { Rt } \triangle A E O $ 中, 由勾股定理, 得 $ A E ^ { 2 } + O E ^ { 2 } = O A ^ { 2 } $, 即 $ 4 ^ { 2 } + ( r - 2 ) ^ { 2 } = r ^ { 2 } $, 解得 $ r = 5 $. $ \therefore A B = 2 r = 10 $. 在 $ \mathrm { Rt } \triangle A C B $ 中, 由勾股定理, 得 $ B C = \sqrt { A B ^ { 2 } - A C ^ { 2 } } = \sqrt { 10 ^ { 2 } - 8 ^ { 2 } } = 6 $, $ \therefore B F = B C + C F = 8 $. 在 $ \mathrm { Rt } \triangle B F D $ 中, 由勾股定理, 得 $ B D = \sqrt { B F ^ { 2 } + D F ^ { 2 } } = \sqrt { 8 ^ { 2 } + 4 ^ { 2 } } = 4 \sqrt { 5 } $.
14. (8分)如图,在$△ABC$中,以AB为直径的$\odot O$分别与BC,AC相交于点D,E,$BD=CD$,过点D作$\odot O$的切线交边AC于点F.
(1)求证:$DF⊥AC$;
(2)若$\odot O$的半径为5,$∠CDF=30^{\circ }$,则$\widehat {BD}$的长为
(1)求证:$DF⊥AC$;
(2)若$\odot O$的半径为5,$∠CDF=30^{\circ }$,则$\widehat {BD}$的长为
$\frac {5}{3}\pi$
.(结果保留π)
答案:
解:
(1) 连接 $ O D $. $ \because D F $ 是 $ \odot O $ 的切线, $ D $ 为切点, $ \therefore O D \perp D F $, $ \therefore \angle O D F = 90 ^ { \circ } $. $ \because B D = C D $, $ O A = O B $, $ \therefore O D $ 是 $ \triangle A B C $ 的中位线, $ \therefore O D // A C $, $ \therefore \angle C F D = \angle O D F = 90 ^ { \circ } $, $ \therefore D F \perp A C $;
(2) $ \frac { 5 } { 3 } \pi $
(1) 连接 $ O D $. $ \because D F $ 是 $ \odot O $ 的切线, $ D $ 为切点, $ \therefore O D \perp D F $, $ \therefore \angle O D F = 90 ^ { \circ } $. $ \because B D = C D $, $ O A = O B $, $ \therefore O D $ 是 $ \triangle A B C $ 的中位线, $ \therefore O D // A C $, $ \therefore \angle C F D = \angle O D F = 90 ^ { \circ } $, $ \therefore D F \perp A C $;
(2) $ \frac { 5 } { 3 } \pi $
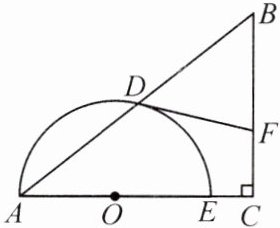
15. (8分)如图,在$Rt△ABC$中,$∠C=90^{\circ }$,点O在AC上,以OA长为半径的半圆O交AB于点D,交AC于点E,过点D作半圆O的切线DF,交BC于点F.
(1)求证:$BF=DF$;
(2)若$AC=4,BC=3,CF=1$,求半圆O的半径.
(1)求证:$BF=DF$;
(2)若$AC=4,BC=3,CF=1$,求半圆O的半径.

答案:
解:
(1) 连接 $ O D $. $ \because D F $ 是 $ \odot O $ 的切线, $ \therefore \angle O D F = 90 ^ { \circ } $, $ \therefore \angle A D O + \angle B D F = 90 ^ { \circ } $. $ \because O A = O D $, $ \therefore \angle O A D = \angle O D A $, $ \therefore \angle O A D + \angle B D F = 90 ^ { \circ } $. $ \because \angle C = 90 ^ { \circ } $, $ \therefore \angle O A D + \angle B = 90 ^ { \circ } $, $ \therefore \angle B = \angle B D F $, $ \therefore B F = D F $;
(2) 连接 $ O F $. 设半圆 $ O $ 的半径为 $ r $, 则 $ O D = O A = r $. $ \because A C = 4 $, $ B C = 3 $, $ C F = 1 $, $ \therefore O C = 4 - r $, $ D F = B F = 3 - 1 = 2 $. 由勾股定理, 得 $ O D ^ { 2 } + D F ^ { 2 } = O F ^ { 2 } = O C ^ { 2 } + C F ^ { 2 } $, $ \therefore r ^ { 2 } + 2 ^ { 2 } = ( 4 - r ) ^ { 2 } + 1 ^ { 2 } $, $ \therefore r = \frac { 13 } { 8 } $. 故半圆 $ O $ 的半径为 $ \frac { 13 } { 8 } $.
(1) 连接 $ O D $. $ \because D F $ 是 $ \odot O $ 的切线, $ \therefore \angle O D F = 90 ^ { \circ } $, $ \therefore \angle A D O + \angle B D F = 90 ^ { \circ } $. $ \because O A = O D $, $ \therefore \angle O A D = \angle O D A $, $ \therefore \angle O A D + \angle B D F = 90 ^ { \circ } $. $ \because \angle C = 90 ^ { \circ } $, $ \therefore \angle O A D + \angle B = 90 ^ { \circ } $, $ \therefore \angle B = \angle B D F $, $ \therefore B F = D F $;
(2) 连接 $ O F $. 设半圆 $ O $ 的半径为 $ r $, 则 $ O D = O A = r $. $ \because A C = 4 $, $ B C = 3 $, $ C F = 1 $, $ \therefore O C = 4 - r $, $ D F = B F = 3 - 1 = 2 $. 由勾股定理, 得 $ O D ^ { 2 } + D F ^ { 2 } = O F ^ { 2 } = O C ^ { 2 } + C F ^ { 2 } $, $ \therefore r ^ { 2 } + 2 ^ { 2 } = ( 4 - r ) ^ { 2 } + 1 ^ { 2 } $, $ \therefore r = \frac { 13 } { 8 } $. 故半圆 $ O $ 的半径为 $ \frac { 13 } { 8 } $.
查看更多完整答案,请扫码查看


