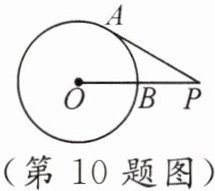
10. 如图,点$P$为$\odot O$外一点,$PA$为$\odot O$的切线,$A$为切点,$PO$交于$\odot O$于点$B$,$\angle P=30^{\circ}$,$OB=3$,则线段$BP$的长为
3
.
答案:
3
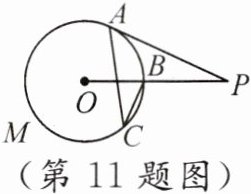
11. 如图,$PA$与$\odot O$相切于点$A$,$PO$与$\odot O$相交于点$B$,点$C$在$\overset{\frown}{AMB}$上,且与点$A$,$B$不重合.若$\angle P=26^{\circ}$,则$\angle C$的度数为____
$32^{\circ}$
.
答案:
$ 32 ^ { \circ } $
12. 如图,已知$\triangle ABE$为直角三角形,$\angle ABE=90^{\circ}$,$BC$为$\odot O$的切线,$C$为切点,$CA=CD$,则$\triangle ABC$和$\triangle CDE$的面积之比为
$1:2$
.
答案:
$ 1 : 2 $
13. (8 分)如图,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$D$是$AB$上的一点,以$AD$为直径的$\odot O$与$BC$相切于点$E$,连接$AE$.
求证:$AE$平分$\angle BAC$.

求证:$AE$平分$\angle BAC$.

答案:
证明:连接 $ O E $. $ \because \odot O $ 与 $ B C $ 相切于点 $ E $, $ \therefore O E \perp B C $, 即 $ \angle O E B = 90 ^ { \circ } $. 又 $ \because \angle C = 90 ^ { \circ } $, $ \therefore \angle O E B = \angle C $, $ \therefore O E // A C $, $ \therefore \angle O E A = \angle E A C $. $ \because O E = O A $, $ \therefore \angle O E A = \angle O A E $, $ \therefore \angle O A E = \angle E A C $, 即 $ A E $ 平分 $ \angle B A C $.
14. (8 分)如图,$\angle A=90^{\circ}$,$\odot O$是$\triangle ABC$的内切圆,内切圆的半径为 1,与三边的切点分别是点$E$,$F$,$D$,$AC=4$,求$AB$,$BC$的长.


答案:
解:连接 $ O E $, $ O F $. $ \because \odot O $ 是 $ \triangle A B C $ 的内切圆, 与三边的切点分别是 $ E $, $ F $, $ D $, $ \therefore \angle A E O = \angle A F O = 90 ^ { \circ } $. $ \because \angle A = 90 ^ { \circ } $, $ \therefore $ 四边形 $ A E O F $ 是矩形. 又 $ \because O E = O F = 1 $, $ \therefore $ 四边形 $ A E O F $ 是正方形, $ \therefore A E = A F = O E = O F = 1 $. 设 $ B E = x $, 则 $ B D = B E = x $. 又 $ \because A F = 1 $, $ A C = 4 $, $ \therefore C D = C F = 3 $. 在 $ \mathrm { Rt } \triangle A B C $ 中, 由勾股定理, 得 $ A B ^ { 2 } + A C ^ { 2 } = B C ^ { 2 } $, 即 $ ( x + 1 ) ^ { 2 } + 4 ^ { 2 } = ( x + 3 ) ^ { 2 } $, 解得 $ x = 2 $. $ \therefore A B = x + 1 = 3 $, $ B C = x + 3 = 5 $.
15. (8 分)如图,在$\triangle ABC$中,$AB=AC$,以$AB$为直径作$\odot O$,交$BC$于点$D$,交$CA$的延长线于点$E$,连接$AD$,$DE$.
(1)求证:$D$是$BC$的中点;
(2)若$DE=4$,$AD=2$,求$\odot O$的半径.

(1)求证:$D$是$BC$的中点;
(2)若$DE=4$,$AD=2$,求$\odot O$的半径.

答案:
解:
(1) $ \because A B $ 是 $ \odot O $ 的直径, $ \therefore \angle A D B = 90 ^ { \circ } $, $ \therefore A D \perp B C $. 又 $ \because A B = A C $, $ \therefore D B = D C $, 即 $ D $ 是 $ B C $ 的中点;
(2) $ \because A B = A C $, $ \therefore \angle B = \angle C $. 又 $ \because \angle B = \angle E $, $ \therefore \angle C = \angle E $, $ \therefore D E = D C $. $ \because D C = D B $, $ D E = 4 $, $ \therefore D B = D E = 4 $. 在 $ \mathrm { Rt } \triangle A D B $ 中, 由勾股定理, 得 $ A B = \sqrt { A D ^ { 2 } + D B ^ { 2 } } = \sqrt { 2 ^ { 2 } + 4 ^ { 2 } } = 2 \sqrt { 5 } $, $ \therefore \odot O $ 的半径为 $ \frac { 2 \sqrt { 5 } } { 2 } = \sqrt { 5 } $.
(1) $ \because A B $ 是 $ \odot O $ 的直径, $ \therefore \angle A D B = 90 ^ { \circ } $, $ \therefore A D \perp B C $. 又 $ \because A B = A C $, $ \therefore D B = D C $, 即 $ D $ 是 $ B C $ 的中点;
(2) $ \because A B = A C $, $ \therefore \angle B = \angle C $. 又 $ \because \angle B = \angle E $, $ \therefore \angle C = \angle E $, $ \therefore D E = D C $. $ \because D C = D B $, $ D E = 4 $, $ \therefore D B = D E = 4 $. 在 $ \mathrm { Rt } \triangle A D B $ 中, 由勾股定理, 得 $ A B = \sqrt { A D ^ { 2 } + D B ^ { 2 } } = \sqrt { 2 ^ { 2 } + 4 ^ { 2 } } = 2 \sqrt { 5 } $, $ \therefore \odot O $ 的半径为 $ \frac { 2 \sqrt { 5 } } { 2 } = \sqrt { 5 } $.
查看更多完整答案,请扫码查看


