1. 下列图形中,既是轴对称图形又是中心对称图形的是 (
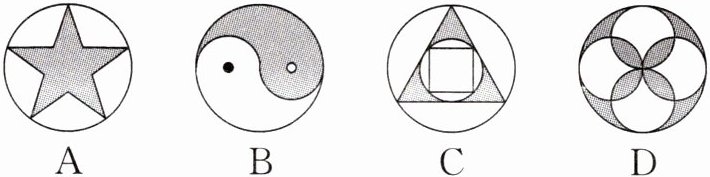
D
)
答案:
D
2. 如图,$△ABC$与$△A'B'C'$成中心对称,下列说法不正确的是 (

A. $S_{△ABC}=S_{△A'B'C'}$
B. $AB=A'B',AC=A'C',BC=B'C'$
C. $AB// A'B',AC// A'C',BC// B'C'$
D. $S_{△ACO}=S_{△A'B'O}$
D
)
A. $S_{△ABC}=S_{△A'B'C'}$
B. $AB=A'B',AC=A'C',BC=B'C'$
C. $AB// A'B',AC// A'C',BC// B'C'$
D. $S_{△ACO}=S_{△A'B'O}$
答案:
D
3. 若点$P(3a,4)$与点$Q(-3,2b)$关于坐标原点对称,则$a,b$的值分别为 (
A. $-1,2$
B. $1,-2$
C. $1,2$
D. $-1,-2$
B
)A. $-1,2$
B. $1,-2$
C. $1,2$
D. $-1,-2$
答案:
B
4. 将如图所示的图案绕其中心旋转$n^{\circ}$时与原图案完全重合,那么$n$的最小值是(

A. $60$
B. $90$
C. $120$
D. $180$
C
)
A. $60$
B. $90$
C. $120$
D. $180$
答案:
C
5. 如图,将图中的$Rt△ABC$向右翻滚,下列说法正确的有 (

(1)$①→②$是旋转;(2)$①→③$是平移;
(3)$①→④$是平移;(4)$②→③$是旋转.
A. $1$个
B. $2$个
C. $3$个
D. $4$个
C
)
(1)$①→②$是旋转;(2)$①→③$是平移;
(3)$①→④$是平移;(4)$②→③$是旋转.
A. $1$个
B. $2$个
C. $3$个
D. $4$个
答案:
C
6. 如图,将$△ABC$先向右平移$1$个单位长度,再绕点$P$按顺时针方向旋转$90^{\circ}$,得到$△A'B'C'$,则点$B$的对应点$B'$的坐标是 (
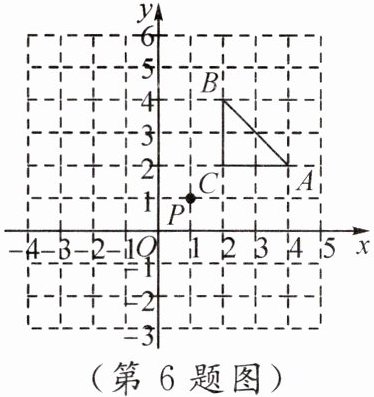
A. $(4,0)$
B. $(2,-2)$
C. $(4,-1)$
D. $(2,-3)$
C
)
A. $(4,0)$
B. $(2,-2)$
C. $(4,-1)$
D. $(2,-3)$
答案:
C
7. 如图,$C$是线段$BD$上一点,分别以$BC$,$CD$为边在$BD$同侧作等边三角形$ABC$和等边三角形$CDE$,$AD$交$CE$于点$F$,$BE$交$AC$于点$G$,则图中可通过旋转而相互得到的三角形有 (
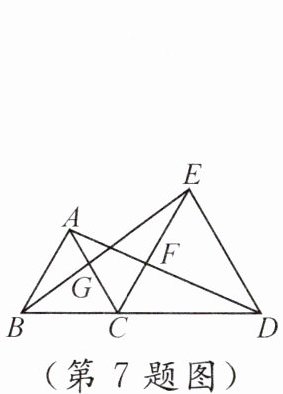
A. $1$对
B. $2$对
C. $3$对
D. $4$对
C
)
A. $1$对
B. $2$对
C. $3$对
D. $4$对
答案:
C
8. 如图,已知四边形$OABC$关于$x$轴对称,$∠AOC=60^{\circ},∠ABC=90^{\circ},OA=2$,将四边形$OABC$绕点$O$逆时针旋转$90^{\circ}$后得到四边形$OA_{1}B_{1}C_{1}$.依此方式,绕点$O$连续旋转$2025$次得到四边形$OA_{2025}B_{2025}C_{2025}$,那么点$B_{2025}$的坐标是 (
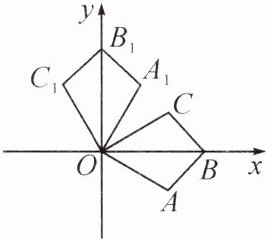
A. $(0,\sqrt{3}+1)$
B. $(\sqrt{3}+1,0)$
C. $(0,-\sqrt{3}-1)$
D. $(-\sqrt{3}-1,0)$
A
)
A. $(0,\sqrt{3}+1)$
B. $(\sqrt{3}+1,0)$
C. $(0,-\sqrt{3}-1)$
D. $(-\sqrt{3}-1,0)$
答案:
A
9. 如图,$②③④⑤$可以看成由$①$经过某种图形变换得到的,其中$②$是由$①$

旋转
得到的;$③$是由$①$平移
得到的;$④$是由$①$轴对称
得到的;$⑤$是由$①$旋转
得到的.(均选填“平移”“轴对称”或“旋转”)
答案:
旋转 平移 轴对称 旋转
查看更多完整答案,请扫码查看


