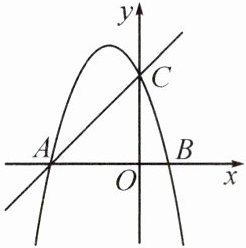
1. 如图,抛物线$y=-x^{2}-2x+3$与x轴交于点A,B(点A在点B左侧),与y轴交于点C.若点P是线段AC上方抛物线上一动点,则$\triangle PAC$的面积最大值是
$\frac{27}{8}$
.
答案:
$\frac{27}{8}$
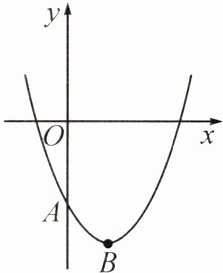
2. 如图,已知抛物线$y=a(x-1)^{2}-3$与y轴交于点$A(0,-2)$,顶点为B.
(1)求抛物线的函数解析式,并写出顶点B的坐标;
(2)试在x轴上求一点P,使得$\triangle PAB$的周长最小.
(1)求抛物线的函数解析式,并写出顶点B的坐标;
(2)试在x轴上求一点P,使得$\triangle PAB$的周长最小.

答案:
解:
(1) 把 $A(0,-2)$ 代入 $y = a(x - 1)^2 - 3$, 得 $a - 3 = -2$, 解得 $a = 1$.
∴ 抛物线的函数解析式为 $y = (x - 1)^2 - 3$; $B(1,-3)$;
(2) 设点 $A$ 关于 $x$ 轴的对称点为 $C$, 则 $C(0,2)$. 连接 $CB$, 交 $x$ 轴于点 $P$, 连接 $AP, AB$, 此时 $\triangle PAB$ 的周长最小. 设直线 $CB$ 的解析式为 $y = mx + n$. 把 $C(0,2)$ 和 $B(1,-3)$ 代入, 得 $\begin{cases}2 = n,\\-3 = m + n,\end{cases}$ 解得 $\begin{cases}m = -5,\\n = 2.\end{cases}$
∴ 直线 $CB$ 的解析式为 $y = -5x + 2$. 把 $y = 0$ 代入 $y = -5x + 2$, 得 $0 = -5x + 2$, 解得 $x = \frac{2}{5}$.
∴ 点 $P$ 的坐标为 $(\frac{2}{5},0)$.
(1) 把 $A(0,-2)$ 代入 $y = a(x - 1)^2 - 3$, 得 $a - 3 = -2$, 解得 $a = 1$.
∴ 抛物线的函数解析式为 $y = (x - 1)^2 - 3$; $B(1,-3)$;
(2) 设点 $A$ 关于 $x$ 轴的对称点为 $C$, 则 $C(0,2)$. 连接 $CB$, 交 $x$ 轴于点 $P$, 连接 $AP, AB$, 此时 $\triangle PAB$ 的周长最小. 设直线 $CB$ 的解析式为 $y = mx + n$. 把 $C(0,2)$ 和 $B(1,-3)$ 代入, 得 $\begin{cases}2 = n,\\-3 = m + n,\end{cases}$ 解得 $\begin{cases}m = -5,\\n = 2.\end{cases}$
∴ 直线 $CB$ 的解析式为 $y = -5x + 2$. 把 $y = 0$ 代入 $y = -5x + 2$, 得 $0 = -5x + 2$, 解得 $x = \frac{2}{5}$.
∴ 点 $P$ 的坐标为 $(\frac{2}{5},0)$.
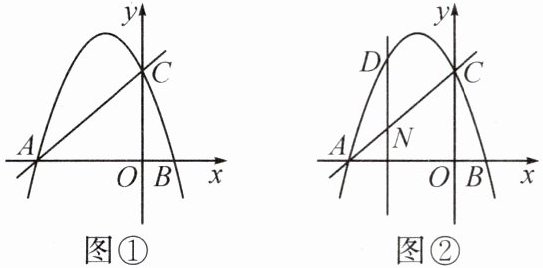
3. 如图①,抛物线$y=-x^{2}+bx+c$交x轴于点$A(-2,0)$和点B,交y轴于点$C(0,2)$.
(1)抛物线的函数解析式为
(2)若点M在抛物线上,且$S_{\triangle AOM}=2S_{\triangle BOC}$,求点M的坐标;
(3)如图②,设点N是线段AC上的一动点,作$DN\perp x$轴,交抛物线于点D,求线段DN长度的最大值.
(1)抛物线的函数解析式为
$y=-x^{2}-x+2$
;(2)若点M在抛物线上,且$S_{\triangle AOM}=2S_{\triangle BOC}$,求点M的坐标;
$(\frac{-1+\sqrt{17}}{2},-2)$或$(\frac{-1-\sqrt{17}}{2},-2)$或$(0,2)$或$(-1,2)$
(3)如图②,设点N是线段AC上的一动点,作$DN\perp x$轴,交抛物线于点D,求线段DN长度的最大值.
1

答案:
解:
(1) $y = -x^2 - x + 2$
(2) 由
(1), 得此抛物线的解析式为 $y = -x^2 - x + 2$, 令 $y = 0$, 得 $B(1,0)$. 设 $M(m,-m^2 - m + 2)$. 根据 $S_{\triangle AOM} = 2S_{\triangle BOC}$, 得 $\frac{1}{2}AO \cdot |-m^2 - m + 2| = 2 \times \frac{1}{2}BO \cdot CO$,
∴ $\frac{1}{2} \times 2 \times |-m^2 - m + 2| = 2$,
∴ $|m^2 + m - 2| = 2$,
∴ $m^2 + m - 2 = 2$ 或 $m^2 + m - 2 = -2$, 解得 $m = \frac{-1 \pm \sqrt{17}}{2}$ 或 $0$ 或 $-1$,
∴ 点 $M$ 的坐标为 $(\frac{-1 + \sqrt{17}}{2},-2)$ 或 $(\frac{-1 - \sqrt{17}}{2},-2)$ 或 $(0,2)$ 或 $(-1,2)$;
(3) 易得直线 $AC$ 的解析式为 $y = x + 2$. 设 $N(a,a + 2)(-2 \leq a \leq 0)$, 则 $D(a,-a^2 - a + 2)$,
∴ $DN = (-a^2 - a + 2) - (a + 2) = -a^2 - 2a = -(a + 1)^2 + 1$.
∵ $-2 < -1 < 0$,
∴ 当 $a = -1$ 时, $DN$ 有最大值, 最大值为 $1$.
(1) $y = -x^2 - x + 2$
(2) 由
(1), 得此抛物线的解析式为 $y = -x^2 - x + 2$, 令 $y = 0$, 得 $B(1,0)$. 设 $M(m,-m^2 - m + 2)$. 根据 $S_{\triangle AOM} = 2S_{\triangle BOC}$, 得 $\frac{1}{2}AO \cdot |-m^2 - m + 2| = 2 \times \frac{1}{2}BO \cdot CO$,
∴ $\frac{1}{2} \times 2 \times |-m^2 - m + 2| = 2$,
∴ $|m^2 + m - 2| = 2$,
∴ $m^2 + m - 2 = 2$ 或 $m^2 + m - 2 = -2$, 解得 $m = \frac{-1 \pm \sqrt{17}}{2}$ 或 $0$ 或 $-1$,
∴ 点 $M$ 的坐标为 $(\frac{-1 + \sqrt{17}}{2},-2)$ 或 $(\frac{-1 - \sqrt{17}}{2},-2)$ 或 $(0,2)$ 或 $(-1,2)$;
(3) 易得直线 $AC$ 的解析式为 $y = x + 2$. 设 $N(a,a + 2)(-2 \leq a \leq 0)$, 则 $D(a,-a^2 - a + 2)$,
∴ $DN = (-a^2 - a + 2) - (a + 2) = -a^2 - 2a = -(a + 1)^2 + 1$.
∵ $-2 < -1 < 0$,
∴ 当 $a = -1$ 时, $DN$ 有最大值, 最大值为 $1$.
查看更多完整答案,请扫码查看


