《2025年一对一同步精练测评五年级数学下册西师大版》

1. 方程的解就是解方程。 (　　　)

答案： ×

2. 解方程$x + 7 = 12$时,方程两边要同时减7。 (　　　)

答案： √

3. 方程$5x = 0$没有解。 (　　　)

答案： ×

二、根据等式的性质,在〇里填运算符号,在□里填数。
1. $x + 3 = 15$
解:$x + 3$〇□$ = 15$〇□
$x =$□
2. $4y = 5.2$
解:$4y$〇□$ = 5.2$〇□
$y =$□
3. $m - \frac{1}{2} = \frac{1}{4}$
解:$m - \frac{1}{2}$〇□$ = \frac{1}{4}$〇□
$m =$□
4. $n\div4.5 = 6$
解:$n\div4.5$〇□$ = 6$〇□
$n =$□

答案： 1. -；3；-；3；12
2. ÷；4；÷；4；1.3
3. +；$\frac{1}{2}$；+；$\frac{1}{2}$；$\frac{3}{4}$
4. ×；4.5；×；4.5；27

三、解方程,带*的要求检验。
$x - 3 = 16$ *$x + 1.8 = 3.5$ $x\div0.5 = 0.7$
$1.2x = 9.6$ $\frac{4}{7} + y = \frac{3}{4}$ *$x\div1.8 = 41$

答案： $x - 3 = 16$
解:$x - 3 + 3 = 16 + 3$
$x = 19$
*$x + 1.8 = 3.5$
解:$x + 1.8 - 1.8 = 3.5 - 1.8$
$x = 1.7$
检验:把$x = 1.7$代入原方程,
左边$ = 1.7 + 1.8 = 3.5$,右边$ = 3.5$,
左边$ = $右边,
所以$x = 1.7$是原方程的解。
$x\div0.5 = 0.7$
解:$x\div0.5\times0.5 = 0.7\times0.5$
$x = 0.35$
$1.2x = 9.6$
解:$1.2x\div1.2 = 9.6\div1.2$
$x = 8$
$\frac{4}{7} + y = \frac{3}{4}$
解:$\frac{4}{7} + y - \frac{4}{7} = \frac{3}{4} - \frac{4}{7}$
$y = \frac{5}{28}$
*$x\div1.8 = 41$
解:$x\div1.8\times1.8 = 41\times1.8$
$x = 73.8$
检验:把$x = 73.8$代入原方程,
左边$ = 73.8\div1.8 = 41$,右边$ = 41$,
左边$ = $右边,
所以$x = 73.8$是原方程的解。

四、看图列方程,并求出方程的解。

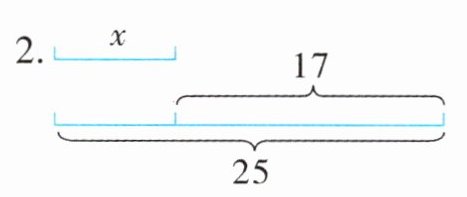
答案： 1. $5x = 22.5$ $x = 4.5$ 2. $x + 17 = 25$ $x = 8$ 

五、方程$x - 1.2 = 2.8$与$bx = 3.2$有相同的解,求$b$的值。

答案： 先解方程$x - 1.2 = 2.8$
$x - 1.2 + 1.2 = 2.8 + 1.2$
$x = 4$
把$x = 4$代入$bx = 3.2$得$4b = 3.2$
$4b\div4 = 3.2\div4$
$b = 0.8$