1. 一个蓄水池能蓄水 1080L,这个蓄水池长 24dm,宽 5dm,深( )dm。
A. 9
B. 12
C. 45
A. 9
B. 12
C. 45
答案:
A
2. 一个长方体的长、宽、高分别为 am,bm,hm。如果长、宽不变,高增加 3m,那么新长方体的体积比原来增加( )m³。
A. 3ab
B. 3abh
C. (3 + h)ab
A. 3ab
B. 3abh
C. (3 + h)ab
答案:
A
二、家具厂订购 500 根方木,每根方木横截面的面积是 5.4dm²,长是 3m。这些木料一共是多少立方米?
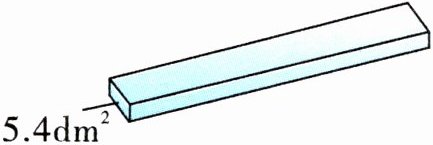

答案:
本题可先将方木横截面面积的单位转换为平方米,再根据长方体体积公式求出一根方木的体积,最后求出$500$根方木的总体积。\n**步骤一:单位换算**
已知$1dm^{2}=0.01m^{2}$,则$5.4dm^{2}$换算为平方米是:$5.4\times0.01 = 0.054m^{2}$。\n**步骤二:计算一根方木的体积**
因为方木可看作长方体,根据长方体的体积公式$V = Sh$(其中$V$为体积,$S$为底面积,$h$为高),已知方木横截面的面积$S = 0.054m^{2}$,长(即高)$h = 3m$,可得一根方木的体积为:$0.054×3 = 0.162$(立方米)。\n**步骤三:计算$500$根方木的总体积**
已知一根方木的体积是$0.162$立方米,那么$500$根方木的总体积为:$0.162×500 = 81$(立方米)。
综上,这些木料一共是$81$立方米。
已知$1dm^{2}=0.01m^{2}$,则$5.4dm^{2}$换算为平方米是:$5.4\times0.01 = 0.054m^{2}$。\n**步骤二:计算一根方木的体积**
因为方木可看作长方体,根据长方体的体积公式$V = Sh$(其中$V$为体积,$S$为底面积,$h$为高),已知方木横截面的面积$S = 0.054m^{2}$,长(即高)$h = 3m$,可得一根方木的体积为:$0.054×3 = 0.162$(立方米)。\n**步骤三:计算$500$根方木的总体积**
已知一根方木的体积是$0.162$立方米,那么$500$根方木的总体积为:$0.162×500 = 81$(立方米)。
综上,这些木料一共是$81$立方米。
三、能把 5 箱这样的食用油(如下图)一并装入一个容积为 3L 的桶中吗?

答案:
本题可先根据长方体体积公式算出$5$箱食用油的总体积,再与桶的容积进行比较,从而判断能否装入。
### 步骤一:计算一箱食用油的体积
由图可知,食用油箱可看作一个长方体,其长$20cm$、宽$10cm$、高$3cm$。
根据长方体体积公式$V = a\times b\times h$(其中$V$为体积,$a$为长,$b$为宽,$h$为高),可得一箱食用油的体积为:
$20\times10\times3 = 600$($cm^3$)
### 步骤二:计算$5$箱食用油的总体积
已知一箱食用油体积为$600cm^3$,那么$5$箱食用油的总体积为:
$600\times5 = 3000$($cm^3$)
### 步骤三:单位换算
因为$1cm^3 = 1ml$,$1L = 1000ml$,所以$3000cm^3 = 3000ml = 3000\div1000 = 3L$。
### 步骤四:比较体积大小
$5$箱食用油的总体积为$3L$,桶的容积也为$3L$,二者体积相等。
所以能把$5$箱这样的食用油一并装入一个容积为$3L$的桶中。
### 步骤一:计算一箱食用油的体积
由图可知,食用油箱可看作一个长方体,其长$20cm$、宽$10cm$、高$3cm$。
根据长方体体积公式$V = a\times b\times h$(其中$V$为体积,$a$为长,$b$为宽,$h$为高),可得一箱食用油的体积为:
$20\times10\times3 = 600$($cm^3$)
### 步骤二:计算$5$箱食用油的总体积
已知一箱食用油体积为$600cm^3$,那么$5$箱食用油的总体积为:
$600\times5 = 3000$($cm^3$)
### 步骤三:单位换算
因为$1cm^3 = 1ml$,$1L = 1000ml$,所以$3000cm^3 = 3000ml = 3000\div1000 = 3L$。
### 步骤四:比较体积大小
$5$箱食用油的总体积为$3L$,桶的容积也为$3L$,二者体积相等。
所以能把$5$箱这样的食用油一并装入一个容积为$3L$的桶中。
四、一种香皂的规格如图所示。厂家要把一批这样的香皂运往外地,包装箱长 45cm,宽 30cm,高 15cm。一个包装箱内最多能装多少块这样的香皂?(包装箱的厚度忽略不计)


答案:
本题可分别计算出包装箱的长、宽、高分别是香皂长、宽、高的倍数,再将这三个倍数相乘,即可得到包装箱内最多能装香皂的块数。
### 步骤一:分析香皂和包装箱的尺寸
由图可知,香皂的长、宽、高分别为$9cm$、$6cm$、$3cm$,包装箱长$45cm$,宽$30cm$,高$15cm$。
### 步骤二:分别计算包装箱的长、宽、高分别是香皂长、宽、高的倍数
- 计算包装箱的长是香皂长的倍数:$45\div9 = 5$(倍)
- 计算包装箱的宽是香皂宽的倍数:$30\div6 = 5$(倍)
- 计算包装箱的高是香皂高的倍数:$15\div3 = 5$(倍)
### 步骤三:计算包装箱内最多能装香皂的块数
将上述三个倍数相乘,可得:$5\times5\times5 = 125$(块)
综上,一个包装箱内最多能装$125$块这样的香皂。
### 步骤一:分析香皂和包装箱的尺寸
由图可知,香皂的长、宽、高分别为$9cm$、$6cm$、$3cm$,包装箱长$45cm$,宽$30cm$,高$15cm$。
### 步骤二:分别计算包装箱的长、宽、高分别是香皂长、宽、高的倍数
- 计算包装箱的长是香皂长的倍数:$45\div9 = 5$(倍)
- 计算包装箱的宽是香皂宽的倍数:$30\div6 = 5$(倍)
- 计算包装箱的高是香皂高的倍数:$15\div3 = 5$(倍)
### 步骤三:计算包装箱内最多能装香皂的块数
将上述三个倍数相乘,可得:$5\times5\times5 = 125$(块)
综上,一个包装箱内最多能装$125$块这样的香皂。
五、求图中石头的体积是多少立方分米。


答案:
本题可根据放入石头后水上升的体积就是石头的体积,利用长方体体积公式来求解。
### 步骤一:分析放入石头前后水的变化情况
由图可知,玻璃缸是一个长方体,放入石头前水的高度为$2dm$,放入石头后水的高度上升到$2.5dm$,那么水上升的高度为:$2.5 - 2 = 0.5dm$。
### 步骤二:确定玻璃缸的底面积
已知玻璃缸的长为$4dm$,宽为$3dm$,根据长方形面积公式$S = a\times b$(其中$S$为面积,$a$为长,$b$为宽),可得玻璃缸的底面积为:$4\times3 = 12dm^{2}$。
### 步骤三:计算石头的体积
因为石头的体积等于上升的水的体积,而上升的水的形状为长方体,其底面积就是玻璃缸的底面积$12dm^{2}$,高为$0.5dm$,根据长方体体积公式$V = S\times h$(其中$V$为体积,$S$为底面积,$h$为高),可得石头的体积为:$12\times0.5 = 6dm^{3}$。
综上,图中石头的体积是$6$立方分米。
### 步骤一:分析放入石头前后水的变化情况
由图可知,玻璃缸是一个长方体,放入石头前水的高度为$2dm$,放入石头后水的高度上升到$2.5dm$,那么水上升的高度为:$2.5 - 2 = 0.5dm$。
### 步骤二:确定玻璃缸的底面积
已知玻璃缸的长为$4dm$,宽为$3dm$,根据长方形面积公式$S = a\times b$(其中$S$为面积,$a$为长,$b$为宽),可得玻璃缸的底面积为:$4\times3 = 12dm^{2}$。
### 步骤三:计算石头的体积
因为石头的体积等于上升的水的体积,而上升的水的形状为长方体,其底面积就是玻璃缸的底面积$12dm^{2}$,高为$0.5dm$,根据长方体体积公式$V = S\times h$(其中$V$为体积,$S$为底面积,$h$为高),可得石头的体积为:$12\times0.5 = 6dm^{3}$。
综上,图中石头的体积是$6$立方分米。
六、妈妈给轩轩买回一张书桌(如下图),它的体积是多少?(单位:dm)
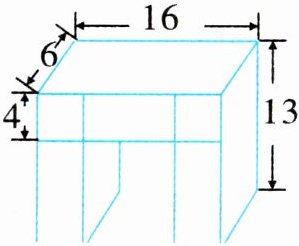

答案:
本题可将书桌看作一个大长方体减去一个小长方体,分别计算出大、小长方体的体积,再用大长方体体积减去小长方体体积,即可得到书桌的体积。
### 步骤一:计算大长方体的体积
由图可知,大长方体的长为$12dm$、宽为$6dm$、高为$3dm$。
根据长方体体积公式$V = a\times b\times h$(其中$V$为体积,$a$为长,$b$为宽,$h$为高),可得大长方体的体积为:
$12\times6\times3 = 216$($dm^3$)
### 步骤二:计算小长方体的体积
由图可知,小长方体的长为$4dm$、宽为$6dm$、高为$1dm$。
同样根据长方体体积公式,可得小长方体的体积为:
$4\times6\times1 = 24$($dm^3$)
### 步骤三:计算书桌的体积
用大长方体的体积减去小长方体的体积,可得书桌的体积为:
$216 - 24 = 192$($dm^3$)
综上,这张书桌的体积是$192dm^3$。
### 步骤一:计算大长方体的体积
由图可知,大长方体的长为$12dm$、宽为$6dm$、高为$3dm$。
根据长方体体积公式$V = a\times b\times h$(其中$V$为体积,$a$为长,$b$为宽,$h$为高),可得大长方体的体积为:
$12\times6\times3 = 216$($dm^3$)
### 步骤二:计算小长方体的体积
由图可知,小长方体的长为$4dm$、宽为$6dm$、高为$1dm$。
同样根据长方体体积公式,可得小长方体的体积为:
$4\times6\times1 = 24$($dm^3$)
### 步骤三:计算书桌的体积
用大长方体的体积减去小长方体的体积,可得书桌的体积为:
$216 - 24 = 192$($dm^3$)
综上,这张书桌的体积是$192dm^3$。
七、把一根长 12dm 的长方体木料平均锯成 3 段,表面积增加了 24dm²,原来这根木料的体积是多少?(损耗忽略不计)


答案:
本题可先根据锯木料的情况求出木料的底面积,再结合木料的长度,利用长方体体积公式求出木料的体积。
### 步骤一:分析锯木料后表面积的变化情况
把长方体木料平均锯成$3$段,需要锯$2$次,每锯一次增加$2$个底面面积,所以锯$2$次共增加了$2\times2 = 4$个底面面积。
### 步骤二:计算木料的底面积
已知表面积增加了$24dm^2$,即$4$个底面面积是$24dm^2$,那么一个底面面积(也就是木料的底面积)为:$24\div4 = 6dm^2$。
### 步骤三:计算木料的体积
根据长方体的体积公式$V = Sh$(其中$V$为体积,$S$为底面积,$h$为高),已知木料的底面积$S = 6dm^2$,长(即高)$h = 12dm$,可得木料的体积为:$6\times12 = 72dm^3$。
综上,原来这根木料的体积是$72dm^3$。
### 步骤一:分析锯木料后表面积的变化情况
把长方体木料平均锯成$3$段,需要锯$2$次,每锯一次增加$2$个底面面积,所以锯$2$次共增加了$2\times2 = 4$个底面面积。
### 步骤二:计算木料的底面积
已知表面积增加了$24dm^2$,即$4$个底面面积是$24dm^2$,那么一个底面面积(也就是木料的底面积)为:$24\div4 = 6dm^2$。
### 步骤三:计算木料的体积
根据长方体的体积公式$V = Sh$(其中$V$为体积,$S$为底面积,$h$为高),已知木料的底面积$S = 6dm^2$,长(即高)$h = 12dm$,可得木料的体积为:$6\times12 = 72dm^3$。
综上,原来这根木料的体积是$72dm^3$。
查看更多完整答案,请扫码查看


