2025年1课3练江苏人民出版社九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1课3练江苏人民出版社九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 二次函数的定义:一般地,形如 ________ (a,b,c 是常数,且 a≠0)的函数叫做二次函数,其中 x 是 ________ ,y 是 x 的函数.
答案:
答案:$y = ax^{2}+bx + c$ 自变量
解析:根据二次函数的定义,形如$y = ax^{2}+bx + c$(a,b,c 是常数,且 a≠0)的函数叫做二次函数,其中 x 是自变量。
解析:根据二次函数的定义,形如$y = ax^{2}+bx + c$(a,b,c 是常数,且 a≠0)的函数叫做二次函数,其中 x 是自变量。
2. 二次函数 y=ax²+bx+c(a≠0)称为二次函数的一般形式,简称一般式,其中二次项系数、一次项系数和常数项分别为 ________ ,________ ,________.
答案:
答案:$a$ $b$ $c$
解析:在二次函数$y = ax^{2}+bx + c$(a≠0)的一般式中,二次项系数是$a$,一次项系数是$b$,常数项是$c$。
解析:在二次函数$y = ax^{2}+bx + c$(a≠0)的一般式中,二次项系数是$a$,一次项系数是$b$,常数项是$c$。
3. (2024·河北秦皇岛期末)下列函数中,y 是 x 的二次函数的是( ).
A. y=$\frac{1}{x^{2}}$
B. y=x²-1
C. y=3x+1
D. y=(x-1)²-x²
A. y=$\frac{1}{x^{2}}$
B. y=x²-1
C. y=3x+1
D. y=(x-1)²-x²
答案:
答案:B
解析:二次函数的一般式是$y = ax^{2}+bx + c$(a≠0)。选项A,$y=\frac{1}{x^{2}}$,自变量在分母上,不是二次函数;选项B,$y = x^{2}-1$,符合二次函数的一般式,是二次函数;选项C,$y = 3x + 1$是一次函数;选项D,$y=(x - 1)^{2}-x^{2}=x^{2}-2x + 1 - x^{2}=-2x + 1$,是一次函数。
解析:二次函数的一般式是$y = ax^{2}+bx + c$(a≠0)。选项A,$y=\frac{1}{x^{2}}$,自变量在分母上,不是二次函数;选项B,$y = x^{2}-1$,符合二次函数的一般式,是二次函数;选项C,$y = 3x + 1$是一次函数;选项D,$y=(x - 1)^{2}-x^{2}=x^{2}-2x + 1 - x^{2}=-2x + 1$,是一次函数。
4. (2024·福建漳州期中)二次函数 y=x²-4x+5 的二次项系数、一次项系数和常数项分别是( ).
A. 1,4,5
B. -1,4,5
C. 1,-4,5
D. -1,-4,5
A. 1,4,5
B. -1,4,5
C. 1,-4,5
D. -1,-4,5
答案:
答案:C
解析:对于二次函数$y = x^{2}-4x + 5$,根据二次函数一般式$y = ax^{2}+bx + c$(a≠0),二次项系数$a = 1$,一次项系数$b=-4$,常数项$c = 5$。
解析:对于二次函数$y = x^{2}-4x + 5$,根据二次函数一般式$y = ax^{2}+bx + c$(a≠0),二次项系数$a = 1$,一次项系数$b=-4$,常数项$c = 5$。
5. 跨学科 自由落体 已知自由落体公式为 h=$\frac{1}{2}$gt²(g 为常量),h 与 t 之间的关系是( ).
A. 正比例函数
B. 一次函数
C. 二次函数
D. 以上答案都不对
A. 正比例函数
B. 一次函数
C. 二次函数
D. 以上答案都不对
答案:
答案:C
解析:二次函数的一般式为$y = ax^{2}+bx + c$(a≠0),在自由落体公式$h=\frac{1}{2}gt^{2}$(g 为常量)中,$a=\frac{1}{2}g$(g 为常量且$g\neq0$,所以$\frac{1}{2}g\neq0$),$b = 0$,$c = 0$,符合二次函数的定义,所以 h 与 t 之间的关系是二次函数。
解析:二次函数的一般式为$y = ax^{2}+bx + c$(a≠0),在自由落体公式$h=\frac{1}{2}gt^{2}$(g 为常量)中,$a=\frac{1}{2}g$(g 为常量且$g\neq0$,所以$\frac{1}{2}g\neq0$),$b = 0$,$c = 0$,符合二次函数的定义,所以 h 与 t 之间的关系是二次函数。
6. 若函数 y=(m-2)x²+5x+6 是二次函数,则有( ).
A. m≠0
B. m≠2
C. x≠0
D. x≠2
A. m≠0
B. m≠2
C. x≠0
D. x≠2
答案:
答案:B
解析:对于二次函数$y = ax^{2}+bx + c$(a≠0),在函数$y=(m - 2)x^{2}+5x + 6$中,要使其为二次函数,则二次项系数$m - 2\neq0$,即$m\neq2$。
解析:对于二次函数$y = ax^{2}+bx + c$(a≠0),在函数$y=(m - 2)x^{2}+5x + 6$中,要使其为二次函数,则二次项系数$m - 2\neq0$,即$m\neq2$。
7. 如图是边长为 5 的正方形 ABCD,点 F 是 BC 上一动点,过对角线交点 E 作 EG⊥EF,交 CD 于点 G,设 BF 的长为 x,△EFG 的面积为 y,则 y 与 x 满足的函数关系是( ).
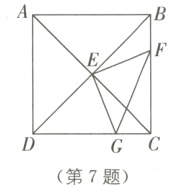
A. 正比例函数
B. 一次函数
C. 二次函数
D. 以上都不是

A. 正比例函数
B. 一次函数
C. 二次函数
D. 以上都不是
答案:
答案:C
解析:通过几何关系可以推导出$\triangle EFG$的面积$y$与$x$的关系式是二次函数形式(具体推导过程需根据正方形的性质和三角形的相关知识,这里省略详细推导),所以$y$与$x$满足的函数关系是二次函数。
解析:通过几何关系可以推导出$\triangle EFG$的面积$y$与$x$的关系式是二次函数形式(具体推导过程需根据正方形的性质和三角形的相关知识,这里省略详细推导),所以$y$与$x$满足的函数关系是二次函数。
8. 如果$ y=x^{t - 2} $是二次函数,那么 t 的值为 ________.
答案:
答案:4
解析:因为二次函数的一般式为$y = ax^{2}+bx + c$(a≠0),对于函数$y = x^{t - 2}$是二次函数,则$t - 2 = 2$,解得$t = 4$。
解析:因为二次函数的一般式为$y = ax^{2}+bx + c$(a≠0),对于函数$y = x^{t - 2}$是二次函数,则$t - 2 = 2$,解得$t = 4$。
9. 若关于 x 的函数 y=(2 - a)x²-3x + 4 是二次函数,则 a 的取值范围是 ________.
答案:
答案:$a\neq2$
解析:对于二次函数$y = ax^{2}+bx + c$(a≠0),在函数$y=(2 - a)x^{2}-3x + 4$中,要使其为二次函数,则二次项系数$2 - a\neq0$,即$a\neq2$。
解析:对于二次函数$y = ax^{2}+bx + c$(a≠0),在函数$y=(2 - a)x^{2}-3x + 4$中,要使其为二次函数,则二次项系数$2 - a\neq0$,即$a\neq2$。
10. 二次函数 y=x²-2x + 3 的一次项系数是 ________.
答案:
答案:$- 2$
解析:对于二次函数$y = x^{2}-2x + 3$,根据二次函数一般式$y = ax^{2}+bx + c$(a≠0),一次项系数是$-2$。
解析:对于二次函数$y = x^{2}-2x + 3$,根据二次函数一般式$y = ax^{2}+bx + c$(a≠0),一次项系数是$-2$。
11. 函数$ y=(m + 2)x^{m² - 2}+2x - 1(x≠0),$当 m = ________ 时,它是二次函数;当 m = ________ 时,它为一次函数.
答案:
答案:$2$ $\pm\sqrt{3}$或$\pm\sqrt{2}$或$-2$
解析:\n若函数为二次函数,则$\begin{cases}m^{2}-2 = 2\\m + 2\neq0\end{cases}$,由$m^{2}-2 = 2$得$m^{2}=4$,解得$m=\pm2$,又因为$m + 2\neq0$,即$m\neq - 2$,所以$m = 2$时,函数是二次函数。\n若函数为一次函数,分三种情况:\n当$m + 2 = 0$,即$m=-2$时,函数为$y = 2x - 1$,是一次函数;\n当$m^{2}-2 = 1$时,$m^{2}=3$,解得$m=\pm\sqrt{3}$,此时函数为一次函数;\n当$m^{2}-2 = 0$时,$m^{2}=2$,解得$m=\pm\sqrt{2}$,此时函数也为一次函数。
解析:\n若函数为二次函数,则$\begin{cases}m^{2}-2 = 2\\m + 2\neq0\end{cases}$,由$m^{2}-2 = 2$得$m^{2}=4$,解得$m=\pm2$,又因为$m + 2\neq0$,即$m\neq - 2$,所以$m = 2$时,函数是二次函数。\n若函数为一次函数,分三种情况:\n当$m + 2 = 0$,即$m=-2$时,函数为$y = 2x - 1$,是一次函数;\n当$m^{2}-2 = 1$时,$m^{2}=3$,解得$m=\pm\sqrt{3}$,此时函数为一次函数;\n当$m^{2}-2 = 0$时,$m^{2}=2$,解得$m=\pm\sqrt{2}$,此时函数也为一次函数。
12. 提分优练 已知$ y=(a - 3)x^{a² - 2a - 1}-2 $是二次函数,求 a 的值.
答案:
答案:$a=-1$
解析:因为函数$y=(a - 3)x^{a^{2}-2a - 1}-2$是二次函数,所以$\begin{cases}a^{2}-2a - 1 = 2\\a - 3\neq0\end{cases}$。
由$a^{2}-2a - 1 = 2$,即$a^{2}-2a - 3 = 0$,因式分解得$(a - 3)(a + 1)=0$,解得$a = 3$或$a=-1$。
又因为$a - 3\neq0$,即$a\neq3$,所以$a=-1$。
解析:因为函数$y=(a - 3)x^{a^{2}-2a - 1}-2$是二次函数,所以$\begin{cases}a^{2}-2a - 1 = 2\\a - 3\neq0\end{cases}$。
由$a^{2}-2a - 1 = 2$,即$a^{2}-2a - 3 = 0$,因式分解得$(a - 3)(a + 1)=0$,解得$a = 3$或$a=-1$。
又因为$a - 3\neq0$,即$a\neq3$,所以$a=-1$。
查看更多完整答案,请扫码查看


