《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1. 直径所对的圆周角是________，90°的圆周角所对的弦是________．

答案： 直角 直径

2. 如果一个四边形的四个顶点都在同一个圆上，这个四边形叫做________，这个圆叫做________________．

答案： 圆内接四边形 四边形的外接圆

3. 圆内接四边形的对角________．

答案： 互补

4. 如图，AB是⊙O的直径，C是⊙O上一点，若∠BAC = 30°，BC = 2，则AC的长为( )．

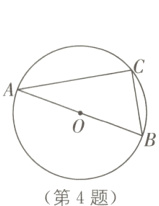
A. 2
B. 4
C. 2√3
D. 4√3

答案： C

5. 如图，在⊙O中，点D，A分别在劣弧BC和优弧BC上，∠BOC = 100°，则∠BDC等于( )．

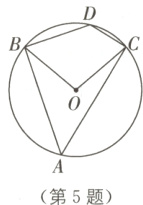
A. 50°
B. 80°
C. 125°
D. 130°

答案： D

6. (2024·天津红桥区期末)如图，AB是⊙O的直径，C，D是⊙O上的两点，若∠ABD = 41°，则∠BCD的大小为( )．

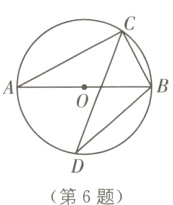
A. 41°
B. 45°
C. 49°
D. 59°

答案： C

7. 如图，AB是⊙O的直径，AB = AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC = 40°，则∠EBC = ________°．

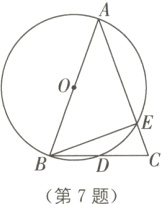
答案： 20

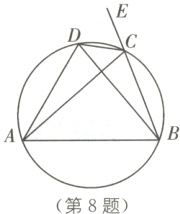
8. 如图，四边形ABCD内接于一圆，CE是边BC的延长线.
(1)求证：∠DAB = ∠DCE；
(2)连接AC，BD，若∠DAB = 60°，∠ACB = 70°，求∠ABD的度数.

答案：
(1)
∵四边形ABCD内接于圆，
∴∠DAB + ∠DCB = 180°.
∵∠DCE + ∠DCB = 180°，
∴∠DAB = ∠DCE.
(2)
∵$\overset{\frown}{AB}=\overset{\frown}{AB}$，
∴∠ADB = ∠ACB = 70°.
∵∠DAB = 60°，
∴∠ABD = 180° - 60° - 70° = 50°.

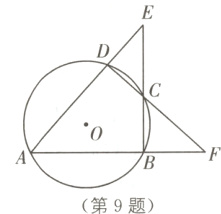
9. 提分优练 中考新考法 满足条件的结论开放 如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F.
(1)若∠E = ∠F，求证：∠ADC = ∠ABC；
(2)当∠E = ∠F = 42°时，求∠A的度数；
(3)若∠E = α，∠F = β，且α≠β，请你用含有α，β的代数式表示∠A的大小.

答案：
(1)
∵∠E = ∠F，∠DCE = ∠BCF，∠ADC = ∠E + ∠DCE，∠ABC = ∠F + ∠BCF，
∴∠ADC = ∠ABC.
(2)由
(1)可知∠ADC = ∠ABC.
∵∠EDC + ∠ADC = 180°，∠ABC + ∠ADC = 180°，
∴∠EDC = ∠ABC，
∴∠EDC = ∠ADC.
∴∠ADC = 90°. 同理可得∠A = ∠DCE，
∴∠A = 90° - 42° = 48°.
(3)连接EF.
∵四边形ABCD为圆的内接四边形
∴∠A + ∠BCD = 180°. 又∠ECD + ∠BCD = 180°，
∴∠ECD = ∠A.
∵∠ECD = ∠CEF + ∠CFE，
∴∠A = ∠CEF + ∠CFE.
∵∠A + ∠CEF + ∠CFE + ∠AEB + ∠AFD = 180°，
∴2∠A + α + β = 180°，即∠A = 90° - $\frac{1}{2}(α + β)$.
易错警示 圆内接四边形的性质是得到角相等关系的重要依据，在应用此性质时，要注意与圆周角定理结合起来. 在应用时要注意是对角互补，而不是邻角互补.