《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1. 体会在实际应用问题中，寻找或构造________，并合理利用锐角三角函数解决问题. 一些常见的三角测量问题可以形成一些模型化的解决方案，注意用心体会.

答案： 直角三角形

2. 能够利用________________以及________测量物体高度.

答案： 相似三角形　勾股定理　直角三角形特殊角

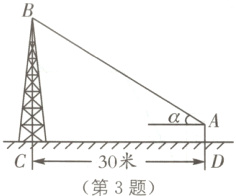
3. 新情境 测量塔高 (2024·广西梧州期末)如图，在离铁塔BC底部30米的D处，用测角仪从点A处测得塔顶B的仰角为α = 30°，测角仪AD高为1.5米，则铁塔的高BC为( ).

A. 16.5米
B. (10√3 + 1.5)米
C. (15√3 + 1.5)米
D. (15√2 + 1.5)米

答案： B

4. (2024·福建泉州实验中学期中)如图，某数学兴趣小组测量一棵树CD的高度，在点A处测得树顶C的仰角为45°，在点B处测得树顶C的仰角为60°，且A，B，D三点在同一直线上，若AB = 16 m，则这棵树CD的高度是( ).

A. 8(3 - √3)m
B. 8(3 + √3)m
C. 6(3 - √3)m
D. 6(3 + √3)m

答案： A

5. (2023·孝感中考)综合实践课上，航模小组用航拍无人机进行测高实践. 如图，无人机从地面CD的中点A处竖直上升30米到达B处，测得博雅楼顶部E的俯角为45°，尚美楼顶部F的俯角为30°，已知博雅楼高度CE为15米，则尚美楼高度DF为______米. (结果保留根号)

答案：
$30 - 5\sqrt{3}$ [解析]如图，过点E作$EM\perp BM$于点M，过点F作$FN\perp BN$于点N.
　　　　　
由题意，得$CM = DN = AB = 30$米.
又$CE = 15$米，$\therefore EM = 15$米.
在$Rt\triangle EBM$中，$\angle EBM = 45^{\circ}$，
$\therefore BM = EM = 15$米.
又A是CD的中点，
$\therefore BN = AD = AC = BM = 15$米，
在$Rt\triangle BFN$中，$\tan\angle FBN=\frac{FN}{BN}$.
$\because\angle FBN = 30^{\circ}$，$BN = 15$米，$\therefore\frac{FN}{15}=\frac{\sqrt{3}}{3}$，
$\therefore FN = 5\sqrt{3}$米，$\therefore DF=(30 - 5\sqrt{3})$米.

6. 提分优练 如图(1)，一台灯放置在水平桌面上，底座AB与桌面垂直，底座高AB = 5 cm，连杆BC = CD = 30 cm，BC，CD与AB始终在同一平面内.
(1)如图(2)，转动连杆BC，CD，使∠BCD成平角，∠ABC = 143°，求连杆端点D离桌面l的高度DE.
(2)将图(2)中的连杆CD再绕点C逆时针旋转16°，如图(3)，此时连杆端点D离桌面l的高度减少了多少厘米? (参考数据：sin 37°≈0.6，cos 37°≈0.8，tan 37°≈0.75)

答案：

(1)如图
(1)，过点B作$BF\perp DE$，垂足为F，
则$AB = EF = 5$cm，$AB// DE$，
$\therefore\angle D = 180^{\circ}-\angle ABC = 37^{\circ}$.
在$Rt\triangle DBF$中，$DB = DC + BC = 60$cm，
$\therefore DF = DB\cdot\cos37^{\circ}\approx60\times0.8 = 48$(cm)，
$\therefore DE = DF + EF = 48 + 5 = 53$(cm).
故连杆端点D离桌面L的高度DE约为53 cm.
　　　　　
(2)如图
(2)，过点D作$DG\perp$桌面L，垂足为G，过点B作$BM\perp DG$，垂足为M，过点C作$CH\perp DG$，垂足为H，过点C作$CN\perp BM$，垂足为N，
则$HM = CN$，$AB = MG = 5$cm，$\angle HCN=\angle CNB=\angle ABM = 90^{\circ}$.
$\because\angle ABC = 143^{\circ}$，
$\therefore\angle CBM=\angle ABC-\angle ABM = 53^{\circ}$，
$\therefore\angle BCN = 90^{\circ}-\angle CBN = 37^{\circ}$.
在$Rt\triangle CNB$中，$BC = 30$cm，
$\therefore CN = BC\cdot\cos37^{\circ}\approx30\times0.8 = 24$(cm)，
$\therefore HM = CN = 24$cm.
在$Rt\triangle DHC$中，$\angle DCH = 180^{\circ}-\angle HCN-\angle BCN - 16^{\circ}= 37^{\circ}$，$DC = 30$cm，
$\therefore DH = DC\cdot\sin37^{\circ}\approx30\times0.6 = 18$(cm)，
$\therefore DG = DH + HM + MG = 18 + 24 + 5 = 47$(cm)，
$\therefore$下降的高度约为$53 - 47 = 6$(cm).
故此时连杆端点D离桌面L的高度减少了约6 cm.