《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1. 我们可以利用一元二次方程解决二次函数的问题，反过来，也可以利用二次函数解决一元二次方程的问题. 比如：可以利用二次函数的________，探究一元二次方程的近似根.

答案： 图象

2. 我们还可以利用二次函数的________，探究一元二次不等式的解集情况.

答案： 图象

3. (2024·江苏南通启东期末)二次函数$y = ax^{2}+bx + c(a\neq0,a,b,c$为常数)中，函数$y$与自变量$x$的部分对应值如下表，则方程$ax^{2}+bx + c = 0$的一个解的范围是( ).
　　　
A. -0.03＜x＜-0.01
B. 3.18＜x＜3.19
C. -0.01＜x＜0.02
D. 3.17＜x＜3.18

答案： B

4. 如图是二次函数$y = ax^{2}+bx + c$图象的一部分，图象过点$A(-5,0)$，对称轴为直线$x = -2$，给出四个结论：①$abc＞0$；②$4a - b = 0$；③若点$B(-3,y_{1})$，$C(0,y_{2})$为函数图象上的两点，则$y_{1}＜y_{2}$；④$a + b + c = 0$.其中，正确结论的个数是( ).
A. 1
B. 2
C. 3
D. 4
　　 　　

答案： C

5. (2024·江苏盐城亭湖区景山中学期末)如图，已知抛物线$y = ax^{2}+c$与直线$y = kx + m$交于$A(-4,y_{1})$，$B(1,y_{2})$两点，则关于$x$的不等式$ax^{2}+c\geqslant kx + m$的解集是________.

答案： $-1\leqslant x\leqslant4$

6. (2024·江苏苏州吴江区期末)二次函数$y = ax^{2}+bx + c(a\neq0,a,b,c$为常数)的图象如图所示，则方程$ax^{2}+bx + c = m$有实数根的条件是________.
　　　　　　　　　　

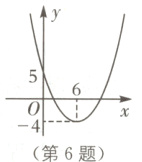
答案： $m\geqslant -4$

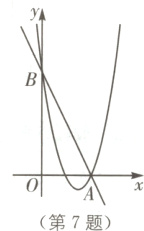
7. 提分优练 中考新考法 数形结合 如图，直线$y = -2x + 8$与$x$轴交于点$A$，与$y$轴交于点$B$，抛物线$y = x^{2}+bx + c$经过点$A$和点$B$.
(1)求抛物线的表达式；
(2)结合图象直接写出不等式$x^{2}+bx + c＞-2x + 8$的解集；
(3)若点$C(1,y_{1})$，$D(m,y_{2})$都在抛物线上，当$y_{2}＞y_{1}$时，求$m$的取值范围.
　　　　　　　　　　　　　　　　

答案：
(1)把$x = 0$代入$y=-2x + 8$，得$y = 8$，
$\therefore$点$B$的坐标为$(0,8)$．
把$y = 0$代入$y=-2x + 8$，得$0=-2x + 8$，
解得$x = 4$，$\therefore$点$A$的坐标为$(4,0)$，
将$(0,8)$，$(4,0)$代入$y=x^{2}+bx + c$，
得$\begin{cases}8 = c\\0 = 16 + 4b + c\end{cases}$，解得$\begin{cases}b=-6\\c = 8\end{cases}$，
$\therefore$抛物线的表达式为$y=x^{2}-6x + 8$．
(2)由图象，得不等式$x^{2}+bx + c＞-2x + 8$的解集为$x＜0$或$x＞4$．
(3)$\because y=x^{2}-6x + 8$，
$\therefore$抛物线对称轴为直线$x=-\frac{-6}{2}=3$，点$C(1,y_{1})$关于对称轴的对称点$C'$坐标为$(5,y_{1})$．
$\because$抛物线开口向上，$\therefore$当$y_{2}＞y_{1}$时，$m＜1$或$m＞5$．