2025年名校真题卷八年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校真题卷八年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
22.(本题12分)定义运算min{a,b}:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{4,0}=0,min{2,2}=2,min{-3,-1}=-3.根据该定义运算回答下列问题:
(1)min{-3,2}=________,当x≤2时,min{x,2}=________;
(2)若min{3x - 1,-x + 3}=-x + 3,求x的取值范围;
(3)如图,直线y1=x + m与y2=kx - 2相交于点P(-2,1),若min{x + m,kx - 2}=x + m,结合图象,直接写出x的取值范围.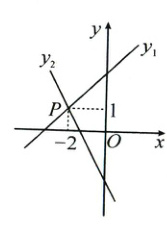
(1)min{-3,2}=________,当x≤2时,min{x,2}=________;
(2)若min{3x - 1,-x + 3}=-x + 3,求x的取值范围;
(3)如图,直线y1=x + m与y2=kx - 2相交于点P(-2,1),若min{x + m,kx - 2}=x + m,结合图象,直接写出x的取值范围.

答案:
解:
(1)$-3$ $x$ [答案详解]根据定义,得$min\{-3,2\} = -3$,当$x\leqslant2$时,$min\{x,2\} = x$.故答案为:$-3$;$x$.
(2)
∵$min\{3x - 1,-x + 3\} = -x + 3$,
∴$3x - 1\geqslant -x + 3$,解得$x\geqslant1$.
(3)
∵$min\{x + m,kx - 2\} = x + m$,
∴根据图象,得$x$的取值范围是$x\leqslant -2$.
(1)$-3$ $x$ [答案详解]根据定义,得$min\{-3,2\} = -3$,当$x\leqslant2$时,$min\{x,2\} = x$.故答案为:$-3$;$x$.
(2)
∵$min\{3x - 1,-x + 3\} = -x + 3$,
∴$3x - 1\geqslant -x + 3$,解得$x\geqslant1$.
(3)
∵$min\{x + m,kx - 2\} = x + m$,
∴根据图象,得$x$的取值范围是$x\leqslant -2$.
23.(本题13分)综合与探究
【问题情境】
数学活动课上,老师带领同学们一起探索旋转的奥秘.老师出示了一个问题:如图1,在△ABC中,AB=AC,∠BAC=90°,D是边BC上一点(0<BD<1/2BC),连接AD,将△ABD绕着点A按逆时针方向旋转,使AB与AC重合,得到△ACE.
【操作探究】
(1)试判断△ADE的形状,并说明理由;
【深入探究】
(2)希望小组受此启发,如图2,在线段CD上取一点F,使得∠DAF=45°,连接EF,发现EF和DF有一定的关系,猜想两者的数量关系,并说明理由;
(3)智慧小组在图2的基础上继续探究,发现线段CF,FD,DB之间也有一定的数量关系.当CF=3,BD=2时,直接写出DF的长.

【问题情境】
数学活动课上,老师带领同学们一起探索旋转的奥秘.老师出示了一个问题:如图1,在△ABC中,AB=AC,∠BAC=90°,D是边BC上一点(0<BD<1/2BC),连接AD,将△ABD绕着点A按逆时针方向旋转,使AB与AC重合,得到△ACE.
【操作探究】
(1)试判断△ADE的形状,并说明理由;
【深入探究】
(2)希望小组受此启发,如图2,在线段CD上取一点F,使得∠DAF=45°,连接EF,发现EF和DF有一定的关系,猜想两者的数量关系,并说明理由;
(3)智慧小组在图2的基础上继续探究,发现线段CF,FD,DB之间也有一定的数量关系.当CF=3,BD=2时,直接写出DF的长.

答案:
解:
(1)$\triangle ADE$为等腰直角三角形.理由如下:由旋转的性质,得$\angle DAE = \angle BAC$,$AD = AE$.
∵$\angle BAC = 90^{\circ}$,
∴$\angle DAE = 90^{\circ}$.
∴$\triangle ADE$为等腰直角三角形.
(2)$EF = DF$.理由如下:
∵$\angle DAE = 90^{\circ}$,$\angle DAF = 45^{\circ}$,
∴$\angle EAF = \angle DAE - \angle DAF = 45^{\circ}$.
∴$\angle EAF = \angle DAF$.又
∵$AF = AF$,$AE = AD$,
∴$\triangle AFE\cong\triangle AFD(SAS)$.
∴$EF = DF$.
(3)
∵$AB = AC$,$\angle BAC = 90^{\circ}$,
∴$\angle B = \angle ACB = 45^{\circ}$.由旋转的性质,得$\angle ACE = \angle B = 45^{\circ}$,$BD = CE = 2$.
∴$\angle BCE = 90^{\circ}$.
∴$EF = CE + CF$.
∵$EF = \sqrt{CF^{2}+CE^{2}} = \sqrt{13}$,
∴$DF = EF = \sqrt{13}$.
(1)$\triangle ADE$为等腰直角三角形.理由如下:由旋转的性质,得$\angle DAE = \angle BAC$,$AD = AE$.
∵$\angle BAC = 90^{\circ}$,
∴$\angle DAE = 90^{\circ}$.
∴$\triangle ADE$为等腰直角三角形.
(2)$EF = DF$.理由如下:
∵$\angle DAE = 90^{\circ}$,$\angle DAF = 45^{\circ}$,
∴$\angle EAF = \angle DAE - \angle DAF = 45^{\circ}$.
∴$\angle EAF = \angle DAF$.又
∵$AF = AF$,$AE = AD$,
∴$\triangle AFE\cong\triangle AFD(SAS)$.
∴$EF = DF$.
(3)
∵$AB = AC$,$\angle BAC = 90^{\circ}$,
∴$\angle B = \angle ACB = 45^{\circ}$.由旋转的性质,得$\angle ACE = \angle B = 45^{\circ}$,$BD = CE = 2$.
∴$\angle BCE = 90^{\circ}$.
∴$EF = CE + CF$.
∵$EF = \sqrt{CF^{2}+CE^{2}} = \sqrt{13}$,
∴$DF = EF = \sqrt{13}$.
查看更多完整答案,请扫码查看


