2025年名校真题卷八年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校真题卷八年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
21.(本题10分)阅读与理解
小林在学习完八年级下册第2章后,结合前面所学知识对“求一元一次不等式的解集”整理得出以下几种方法,请仔细阅读并完成相应的任务.
★年★月★日 星期二 睛
一元一次不等式的解法
引例:求一元一次不等式2x+1>4−x的解集.
方法一:按照七年级解一元一次不等式的步骤求解.(移项,合并同类项,系数化为1)
课本链接:任何一个以x为未知数的一元一次不等式都可以变形为ax十b>0或αx十b<0(a≠0)
的形式,所以解一元一次不等式,相当于求某个一次函数y=αx十b的函数值大于〇或小于0时,自变量r的取值范围.
方法二:将不等式移项,合并同类项,得3x−3>0.如图1,把此不等式的解集看成一个一次函数的图象上取纵坐标大于0的点,看它们的横坐标满足什么条件,由图1可知该不等式的解集为x>1.
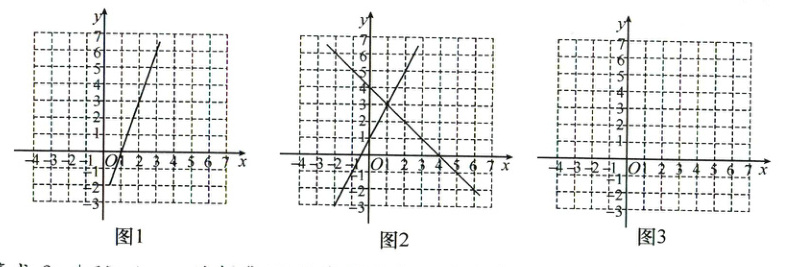
方法三:不等式2x+1>4−x的解集可以看成两个一次函数y1=2x+1和y2=4−x的图象上取纵坐标满足y1>y2的点,看它们的横坐标满足什么条件,由图2可知该不等式的解集为x>1.
任务:
(1)“方法二”和“方法三”共同体现的一个数学思想是____________;
A.整体思想
B.公理化思想
C.数形结合思想
D.分类讨论思想
(2)依据“方法二”的思路,直接写出图1中对应一次函数的表达式为__________________;
(3)参照“方法三”的思路,求一元一次不等式2x−2<$\frac{1}{2}$x+1的解集.请在图3的平面直角坐标系中画出相应的函数图象并依据图象直接写出该不等式的解集.
小林在学习完八年级下册第2章后,结合前面所学知识对“求一元一次不等式的解集”整理得出以下几种方法,请仔细阅读并完成相应的任务.
★年★月★日 星期二 睛
一元一次不等式的解法
引例:求一元一次不等式2x+1>4−x的解集.
方法一:按照七年级解一元一次不等式的步骤求解.(移项,合并同类项,系数化为1)
课本链接:任何一个以x为未知数的一元一次不等式都可以变形为ax十b>0或αx十b<0(a≠0)
的形式,所以解一元一次不等式,相当于求某个一次函数y=αx十b的函数值大于〇或小于0时,自变量r的取值范围.
方法二:将不等式移项,合并同类项,得3x−3>0.如图1,把此不等式的解集看成一个一次函数的图象上取纵坐标大于0的点,看它们的横坐标满足什么条件,由图1可知该不等式的解集为x>1.

方法三:不等式2x+1>4−x的解集可以看成两个一次函数y1=2x+1和y2=4−x的图象上取纵坐标满足y1>y2的点,看它们的横坐标满足什么条件,由图2可知该不等式的解集为x>1.
任务:
(1)“方法二”和“方法三”共同体现的一个数学思想是____________;
A.整体思想
B.公理化思想
C.数形结合思想
D.分类讨论思想
(2)依据“方法二”的思路,直接写出图1中对应一次函数的表达式为__________________;
(3)参照“方法三”的思路,求一元一次不等式2x−2<$\frac{1}{2}$x+1的解集.请在图3的平面直角坐标系中画出相应的函数图象并依据图象直接写出该不等式的解集.
答案:
解:
(1)C
(2)$y = 3x - 3$ [答案详解]
(1)方法二和方法三共同体现数形结合的数学思想.故选:C.
(2)图1中对应一次函数表达式为$y = 3x - 3$.故答案为:$y = 3x - 3$.
(3)如图所示:
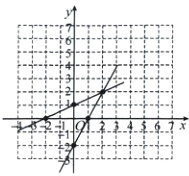
由图象可知,不等式$2x - 2<\frac{1}{2}x + 1$的解集为$x<2$.
解:
(1)C
(2)$y = 3x - 3$ [答案详解]
(1)方法二和方法三共同体现数形结合的数学思想.故选:C.
(2)图1中对应一次函数表达式为$y = 3x - 3$.故答案为:$y = 3x - 3$.
(3)如图所示:

由图象可知,不等式$2x - 2<\frac{1}{2}x + 1$的解集为$x<2$.
22.(本题12分)同学们学习了有理数乘法、不等式组与方程组的知识,它们之间有着一定的逻辑关联,请解决以下问题:
阅读理解:
解不等式:(x + 1)(x - 3)>0.
解:根据两数相乘,同号得正,原不等式可以转化为$\begin{cases}x + 1>0 \\ x - 3>0\end{cases}$或$\begin{cases}x + 1<0 \\ x - 3<0\end{cases}$,解不等式组$\begin{cases}x + 1>0 \\ x - 3>0\end{cases}$得x>3;解不等式组$\begin{cases}x + 1<0 \\ x - 3<0\end{cases}$得x<-1.∴原不等式的解集为x>3或x<-1.
问题解决:
(1)根据以上材料,求不等式(x - 2)(x + 3)<0的解集;
(2)已知关于x,y的二元一次方程组$\begin{cases}x + y = 3 - m \\ x - y = 3m - 1\end{cases}$的解满足xy>0,则m的取值范围为__________.
阅读理解:
解不等式:(x + 1)(x - 3)>0.
解:根据两数相乘,同号得正,原不等式可以转化为$\begin{cases}x + 1>0 \\ x - 3>0\end{cases}$或$\begin{cases}x + 1<0 \\ x - 3<0\end{cases}$,解不等式组$\begin{cases}x + 1>0 \\ x - 3>0\end{cases}$得x>3;解不等式组$\begin{cases}x + 1<0 \\ x - 3<0\end{cases}$得x<-1.∴原不等式的解集为x>3或x<-1.
问题解决:
(1)根据以上材料,求不等式(x - 2)(x + 3)<0的解集;
(2)已知关于x,y的二元一次方程组$\begin{cases}x + y = 3 - m \\ x - y = 3m - 1\end{cases}$的解满足xy>0,则m的取值范围为__________.
答案:
解:
(1)根据两数相乘,异号得负,原不等式可以转化为$\begin{cases}x + 3>0\\x - 2<0\end{cases}$或$\begin{cases}x + 3<0\\x - 2>0\end{cases}$,解不等式组$\begin{cases}x + 3<0\\x - 2>0\end{cases}$,得该不等式组无解;解不等式组$\begin{cases}x + 3>0\\x - 2<0\end{cases}$,得$-3< x<2$,$\therefore $原不等式的解集为$-3< x<2$.
(2)$-1< m<1$ [答案详解]解方程组$\begin{cases}x + y = 3m - 1\\x - y = 3 - m\end{cases}$,得$\begin{cases}x = m + 1\\y = 2m - 2\end{cases}$. $\because xy>0$,$\therefore \begin{cases}x>0\\y>0\end{cases}$或$\begin{cases}x<0\\y<0\end{cases}$,解不等式组$\begin{cases}m + 1>0\\2m - 2>0\end{cases}$,得$-1< m<1$.解不等式组$\begin{cases}m + 1<0\\2m - 2<0\end{cases}$,得此不等式组无解.综上所述,$m$的取值范围是$-1< m<1$.故答案为:$-1 < m<1$.
(1)根据两数相乘,异号得负,原不等式可以转化为$\begin{cases}x + 3>0\\x - 2<0\end{cases}$或$\begin{cases}x + 3<0\\x - 2>0\end{cases}$,解不等式组$\begin{cases}x + 3<0\\x - 2>0\end{cases}$,得该不等式组无解;解不等式组$\begin{cases}x + 3>0\\x - 2<0\end{cases}$,得$-3< x<2$,$\therefore $原不等式的解集为$-3< x<2$.
(2)$-1< m<1$ [答案详解]解方程组$\begin{cases}x + y = 3m - 1\\x - y = 3 - m\end{cases}$,得$\begin{cases}x = m + 1\\y = 2m - 2\end{cases}$. $\because xy>0$,$\therefore \begin{cases}x>0\\y>0\end{cases}$或$\begin{cases}x<0\\y<0\end{cases}$,解不等式组$\begin{cases}m + 1>0\\2m - 2>0\end{cases}$,得$-1< m<1$.解不等式组$\begin{cases}m + 1<0\\2m - 2<0\end{cases}$,得此不等式组无解.综上所述,$m$的取值范围是$-1< m<1$.故答案为:$-1 < m<1$.
查看更多完整答案,请扫码查看


