《2025年名校真题卷八年级数学下册北师大版山西专版》

7. 如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得到△A′BC′.若点C′在AB上,则AA′的长为 ( )
A. $\sqrt{10}$
B. 4
C. 2$\sqrt{5}$
D. 5

答案： A 【答案详解】
∵将△ABC绕点B逆时针旋转得到△A'B'C'，
∴∠A'C'B =∠C =90°，A'C' =AC =3，AB =A'B.根据勾股定理，得AB =$\sqrt{BC^{2}+AC^{2}}$ =5，
∴A'B =AB =5，
∴AC' =A'B - BC' =1.在Rt△AA'C'中，由勾股定理，得AA' =$\sqrt{AC'^{2}+A'C'^{2}}$ =$\sqrt{10}$.故选：A.

8. 如图,在一个高为3米,长为5米的楼梯表面铺地毯,地毯的长度至少是 ( )

A. 3米
B. 4米
C. 5米
D. 7米

答案： D 【答案详解】由勾股定理，得楼梯的水平宽度为$\sqrt{5^{2}-3^{2}}$ =4(米)，
∵地毯铺满楼梯的长度应该是楼梯的水平宽度与垂直高度的和，
∴地毯的长度至少是3 + 4 =7(米).故选：D.

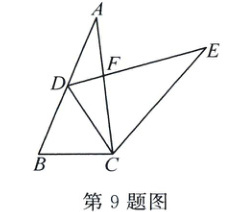
9. 如图,在△ABC中,∠ACB=80°,将△ABC绕点C顺时针旋转得到△EDC,使点B的对应点D恰好落在边AB上,AC,ED相交于点F.若∠BCD=α,则∠EFC的度数是 ( )

A. 80°+$\frac{3}{2}$α
B. 170°+$\frac{3}{2}$α
C. 170°－$\frac{3}{2}$α
D. $\frac{3}{2}$α

答案： C 【答案详解】由旋转的性质可知，BC =CD，∠B =∠EDC，∠A =∠E，∠ACE =∠BCD，
∵∠BCD =α，
∴∠B =∠BDC =$\frac{180^{\circ}-\alpha}{2}$ =90° - $\frac{1}{2}\alpha$，∠ACE =α.
∵∠ACB =80°，
∴∠E =∠A =180° - 80° - ∠B =10° + $\frac{1}{2}\alpha$.
∴∠EFC =180° - ∠ACE - ∠E =170° - $\frac{3}{2}\alpha$.故选：C.

10. 如图,将直角梯形ABCD沿AB方向向下平移2个单位长度得到直角梯形EFGH.已知BC=6,∠A=90°,∠C=45°,则阴影部分的面积为 ( )

A. 8
B. 10
C. 12
D. 5$\sqrt{2}$

答案： B 【答案详解】如图，过点P作PQ⊥FG于点Q.由平移的性质可知，BF =PQ =2，FG =BC =6，$S_{梯形ABCD}$ =$S_{梯形EFGH}$，∠G =∠C =45°，
∴$S_{阴影部分}$ =$S_{梯形ABCD}$ - $S_{梯形EBPH}$ =$S_{梯形EFGH}$ - $S_{梯形EBPH}$ =$S_{梯形BFGP}$.在Rt△PQG中，PQ =2，∠G =45°，
∴QG =PQ =2.
∴BP =FQ =6 - 2 =4.
∴$S_{阴影部分}$ =$S_{梯形BFGP}$ =$\frac{1}{2}$×(4 + 6)×2 =10.故选：B.

11. 将点(1,2)先向右平移1个单位长度，再向下平移3个单位长度，平移后所得点的坐标为______________.

答案： (2,−1) 【答案详解】由题可知，将点(1,2)先向右平移1个单位长度，所得点的坐标为(2,2)，再向下平移3个单位长度，所得点的坐标为(2,−1).故答案为：(2,−1).

12. 如图,在平面直角坐标系xOy中,△OAB是等腰直角三角形,∠OBA=90°,A(8,0)，点B位于第一象限，则点B关于原点的对称点B′的坐标是______________.

答案： (−4,−4). 【答案详解】如图，过点B作BC⊥OC于点C.
∵△OAB是等腰直角三角形，∠OBA =90°，
∴OC =AC =$\frac{1}{2}$OA =4，∠BOA =∠OAB =45°.
∴△OBC是等腰直角三角形.
∴BC =OC =4.
∴B(4,4).
∴点B关于原点的对称点B'的坐标是(−4,−4).故答案为：(−4,−4).

13. 如图,在△ABC中,AB=AC=6 cm，BC=4 cm，将△ABC沿BC方向平移使点B与点C重合，得到△DCE，连接AD，则△ACD的周长为______________ cm.

答案： 16 【答案详解】根据平移的性质，得△ABC≌△DCE，
∴AB =DC =6 cm，AC =DE =6 cm，AD =CE =BC =4 cm.
∴△ACD的周长为AD +AC +CD =4 + 6 + 6 =16(cm).故答案为：16.

14. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,且AB=1,BC=2,则AD的长为______________.

答案： $\sqrt{7}$ 【答案详解】如图，连接BD.由旋转，得CD =BC =2，∠BCD =∠ACE =90°，CA =CE，
∴BD =$\sqrt{2}$BC =2$\sqrt{2}$，∠CAE =∠E =45°.
∴∠CAB =∠E =45°.
∴∠BAD =∠CAB +∠CAE =90°.在Rt△ABD中，AB =1，
∴AD =$\sqrt{BD^{2}-AB^{2}}$ =$\sqrt{(2\sqrt{2})^{2}-1^{2}}$ =$\sqrt{7}$.故答案为：$\sqrt{7}$.

15. 如图,在边长为8的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E的运动过程中,DF的最小值是______________.

答案： 2. 【答案详解】如图，连接BF.由旋转可得，CE =FC，∠ECF =60°，
∵△ABC是等边三角形，
∴AC =BC，∠ACB =60°.
∴∠ACE =∠BCF.在△ACE和△BCF中，$\begin{cases}AC =BC,\\\angle ACE =\angle BCF,\\EC =FC,\end{cases}$
∴△ACE ≌ △BCF(SAS).
∴∠CBF =∠CAE.
∵在边长为8的等边三角形ABC中，E是对称轴AD上的一个动点，
∴∠CAE =30°，BD =4.
∴∠CBF =30°.
∴当DF⊥BF时，DF最短.此时，DF =$\frac{1}{2}$BD =$\frac{1}{2}$×4 =2.
∴DF的最小值是2.故答案为：2.