《2025年名校真题卷八年级数学下册北师大版山西专版》

23.(本题13分)某电器超市销售每台进价分别为160元、120元的A,B两种型号的电风扇,下表是近两周的销售情况:

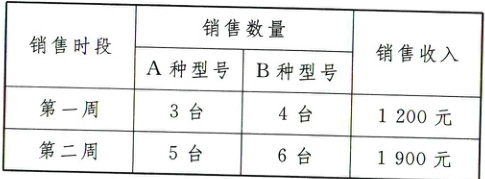
(进价、售价均保持不变,利润 = 销售收入 - 进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台;
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标? 若能,请给出相应的采购方案;若不能,请说明理由.

答案： 解:
(1)设$A$，$B$两种型号电风扇的销售单价分别为$x$元、$y$元.依题意，得$\begin{cases}3x + 4y = 1290\\5x + 6y = 2000\end{cases}$，解得$\begin{cases}x = 220\\y = 150\end{cases}$.答:$A$，$B$两种型号电风扇的销售单价分别为$220$元、$150$元.
(2)设采购$A$种型号电风扇$a$台，则采购$B$种型号的电风扇$(50 - a)$台.依题意，得$160a + 120(50 - a)\leqslant7500$，解得$a\leqslant37\frac{1}{2}$. $\because a$是整数，$\therefore a$的最大值是$37$.答:超市最多采购$A$种型号的电风扇$37$台.
(3)在
(2)的条件下，采购$A$种型号电风扇$a$台，则采购$B$种型号的电风扇$(50 - a)$台.根据题意，得$(220 - 160)a+(150 - 120)(50 - a)＞1850$，解得$a＞35$. $\because a\leqslant37\frac{1}{2}$，且$a$为整数，$\therefore $在
(2)的条件下超市能实现利润超过$1850$元的目标方案有两种:①当$a = 36$时，采购$A$种型号的电风扇$36$台，$B$种型号的电风扇$14$台;②当$a = 37$时，采购$A$种型号的电风扇$37$台，$B$种型号的电风扇$13$台.