第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
6.(2024吉林长春南关期末,18,★★☆)如图,在□ABCD中,延长DC到点E,使CE = DC,连结AE,交BC于点O,∠AOC = 2∠D,连结AC、BE.
求证:四边形ABEC是矩形.(M8219002)
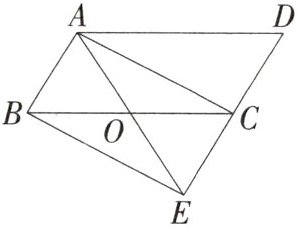
求证:四边形ABEC是矩形.(M8219002)

答案:
**证明**:因为四边形ABCD是平行四边形,所以AB = CD,AB//CD,AD//BC。
因为CE = DC,所以AB = CE,所以四边形ABEC是平行四边形,所以OA = OE,OB = OC。
因为AD//BC,所以∠D = ∠OCE,因为∠AOC = ∠OEC + ∠OCE = 2∠D,所以∠OEC = ∠OCE,所以OE = OC,所以AE = BC,所以四边形ABEC是矩形。
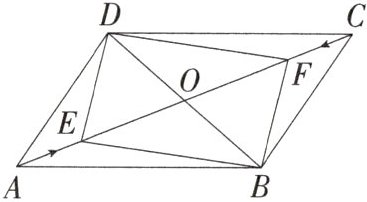
7.(2023重庆沙坪坝期中,20,★★☆)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动,若AC = 12,BD = 8,则经过几秒时,四边形BEDF是矩形?(M8219002)

答案:
**解析**:设点E、F的运动时间均为t秒,则AE = CF = t。
因为四边形ABCD是平行四边形,所以OA = OC=$\frac{1}{2}$AC = 6,OB = OD=$\frac{1}{2}$BD = 4,所以OE = OF,所以四边形BEDF是平行四边形。
当EF = BD,即OE = OD时,四边形BEDF是矩形,此时6 - t = 4或t - 6 = 4,解得t = 2或t = 10,即经过2秒或10秒时,四边形BEDF是矩形。
8.(2022四川巴中中考,21,★★☆)如图,在□ABCD中,E为BC边的中点,连结AE并延长交DC的延长线于点F,延长EC至点G,使CG = CE,连结DG、DE、FG.(M8219002)
(1)求证:△ABE≌△FCE.
(2)若AD = 2AB,求证:四边形DEFG是矩形.
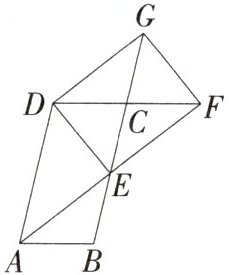
(1)求证:△ABE≌△FCE.
(2)若AD = 2AB,求证:四边形DEFG是矩形.

答案:
**证明**:
(1)因为四边形ABCD是平行四边形,所以AB//CD,所以∠EAB = ∠EFC。
因为E为BC的中点,所以EB = EC。
在△ABE和△FCE中,$\begin{cases}\angle EAB=\angle EFC \\ \angle BEA=\angle CEF \\ EB = EC\end{cases}$,所以△ABE≌△FCE(A.A.S.)。
(2)因为△ABE≌△FCE,所以AB = CF。
因为四边形ABCD是平行四边形,所以AB = DC,AD = BC,所以DC = CF。
又因为CE = CG,所以四边形DEFG是平行四边形。
因为E为BC的中点,CE = CG,所以BC = EG。
因为AD = BC = EG = 2AB,DF = CD + CF = 2CD = 2AB,所以DF = EG,所以平行四边形DEFG是矩形。
9. [模型观念](2023湖北随州中考)如图,在矩形ABCD中,AB = 5,AD = 4,M是边AB上一动点(不含端点),将△ADM沿直线DM翻折,得到△NDM. 当射线CN交线段AB于点P时,连结DP,则△CDP的面积为________,DP的最大值为________.
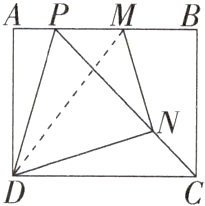

答案:
**答案**:10;$\sqrt{20}$ **解析**:由题图可得△CDP的面积等于矩形ABCD面积的一半,所以△CDP的面积为$\frac{1}{2}$AD·DC = 10。 在Rt△APD中,DP=$\sqrt{AD^{2}+AP^{2}}$,所以当AP最大时,DP最大。 由翻折的性质,得DN = DA = 4,所以点N在以D为圆心,4为半径的圆上运动,如图①。 易得当射线CN⊥DN时,AP最大,此时点P与点M重合,∠DNC = 90°,如图②,所以CN=$\sqrt{5^{2}-4^{2}}$= 3。 由翻折的性质可知PA = PN。设PA = PN = x,则PB = 5 - x,CP = 3 + x。 在Rt△PBC中,由勾股定理,得PB² + BC² = PC²,即(5 - x)² + 4² = (3 + x)²,解得x = 2,所以DP=$\sqrt{4^{2}+2^{2}}$=$\sqrt{20}$。
**答案**:10;$\sqrt{20}$ **解析**:由题图可得△CDP的面积等于矩形ABCD面积的一半,所以△CDP的面积为$\frac{1}{2}$AD·DC = 10。 在Rt△APD中,DP=$\sqrt{AD^{2}+AP^{2}}$,所以当AP最大时,DP最大。 由翻折的性质,得DN = DA = 4,所以点N在以D为圆心,4为半径的圆上运动,如图①。 易得当射线CN⊥DN时,AP最大,此时点P与点M重合,∠DNC = 90°,如图②,所以CN=$\sqrt{5^{2}-4^{2}}$= 3。 由翻折的性质可知PA = PN。设PA = PN = x,则PB = 5 - x,CP = 3 + x。 在Rt△PBC中,由勾股定理,得PB² + BC² = PC²,即(5 - x)² + 4² = (3 + x)²,解得x = 2,所以DP=$\sqrt{4^{2}+2^{2}}$=$\sqrt{20}$。

查看更多完整答案,请扫码查看


