第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
7.(2023 吉林长春二道力旺实验中学期中)已知 A、B 两地之间有一条笔直的公路,甲车从 A 地出发匀速去往 B 地,到达 B 地后立即以原速度原路返回 A 地,乙车从 B 地出发匀速去往 A 地,两车同时出发,乙车比甲车晚 20 分钟到达 A 地. 甲车距 A 地的路程$y$(千米)与甲车行驶的时间$x$(分钟)之间的函数关系如图所示.
(1) 在图中画出乙车距 A 地的路程$y$(千米)与$x$(分钟)之间的函数图象,并求出它所对应的函数关系式.(写出自变量$x$的取值范围)
(2) 甲、乙两车在行驶过程中相遇了_______次.
(3) 求甲车到 B 地时,乙车距 B 地的路程.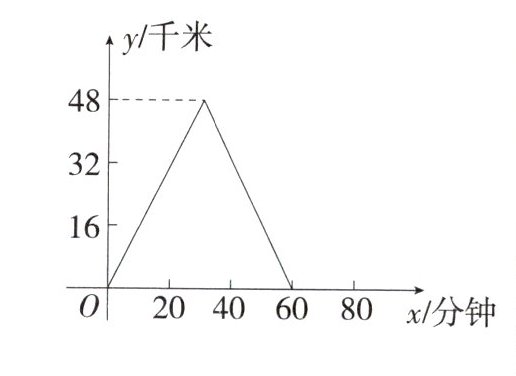
(1) 在图中画出乙车距 A 地的路程$y$(千米)与$x$(分钟)之间的函数图象,并求出它所对应的函数关系式.(写出自变量$x$的取值范围)
(2) 甲、乙两车在行驶过程中相遇了_______次.
(3) 求甲车到 B 地时,乙车距 B 地的路程.

答案:
解析 (1)
∵ 乙车比甲车晚 20 分钟到达 A 地,
∴ 乙车用 80 分钟到达 A 地,画出乙车距 A 地的路程 y(千米)与 x(分钟)之间的函数图象如图所示: ! 设乙车距 A 地的路程 y(千米)与 x(分钟)之间的函数关系式为 y = kx + b(k ≠ 0),
将(0, 48)和(80, 0)代入,得$\begin{cases}b = 48 \\ 80k + b = 0\end{cases}$,
解得$\begin{cases}b = 48 \\ k = -$\frac{3}{5}$\end{cases}$,
设乙车距 A 地的路程 y(千米)与 x(分钟)之间的函数关系式为 y = kx + b(k ≠ 0),
将(0, 48)和(80, 0)代入,得$\begin{cases}b = 48 \\ 80k + b = 0\end{cases}$,
解得$\begin{cases}b = 48 \\ k = -$\frac{3}{5}$\end{cases}$,
∴ y 与 x 之间的函数关系式为 y = -$\frac{3}{5}$x + 48(0 ≤ x ≤ 80)。 (2)两. (3)60÷2 = 30(分钟),
∴ 甲车用 30 分钟到达 B 地, 当 x = 30 时,y = -$\frac{3}{5}$x + 48 = -$\frac{3}{5}$×30 + 48 = 30,48 - 30 = 18(千米)。 答:当甲车到 B 地时,乙车距 B 地的路程为 18 千米。
解析 (1)
∵ 乙车比甲车晚 20 分钟到达 A 地,
∴ 乙车用 80 分钟到达 A 地,画出乙车距 A 地的路程 y(千米)与 x(分钟)之间的函数图象如图所示: !
 设乙车距 A 地的路程 y(千米)与 x(分钟)之间的函数关系式为 y = kx + b(k ≠ 0),
将(0, 48)和(80, 0)代入,得$\begin{cases}b = 48 \\ 80k + b = 0\end{cases}$,
解得$\begin{cases}b = 48 \\ k = -$\frac{3}{5}$\end{cases}$,
设乙车距 A 地的路程 y(千米)与 x(分钟)之间的函数关系式为 y = kx + b(k ≠ 0),
将(0, 48)和(80, 0)代入,得$\begin{cases}b = 48 \\ 80k + b = 0\end{cases}$,
解得$\begin{cases}b = 48 \\ k = -$\frac{3}{5}$\end{cases}$,∴ y 与 x 之间的函数关系式为 y = -$\frac{3}{5}$x + 48(0 ≤ x ≤ 80)。 (2)两. (3)60÷2 = 30(分钟),
∴ 甲车用 30 分钟到达 B 地, 当 x = 30 时,y = -$\frac{3}{5}$x + 48 = -$\frac{3}{5}$×30 + 48 = 30,48 - 30 = 18(千米)。 答:当甲车到 B 地时,乙车距 B 地的路程为 18 千米。
8.(2024 陕西西安阎良三模)【情境描述】
刘欣和妈妈周末去逛超市,发现超市的凳子按如图 1 所示的方式叠放在一起时,每多叠放一个凳子,增加的高度是相同的.
【测量整理】
叠放凳子的总高度$h$(cm)与凳子的数量$n$(个)的部分对应值如表:
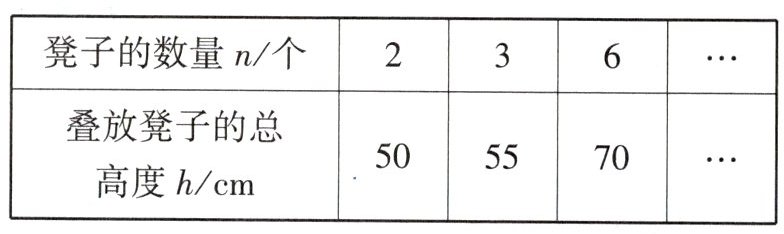
【解决问题】
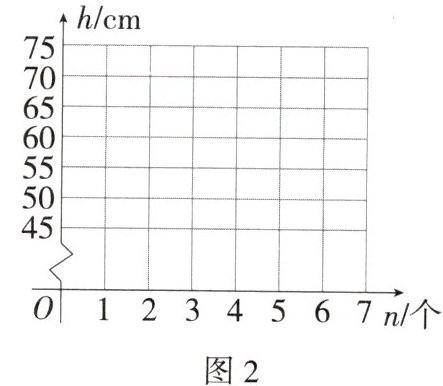
(1) 在图 2 中描出表中对应的点,并顺次连结各点.
(2) 根据图 2 中画出的图象确定符合实际的函数类型,求出$h$关于$n$的函数表达式.(不要求写自变量的取值范围)
(3) 若该超市的一位理货员将 10 个这种凳子叠放在一起,能否将其放入层高为 87 cm 的货架?请说明理由.

刘欣和妈妈周末去逛超市,发现超市的凳子按如图 1 所示的方式叠放在一起时,每多叠放一个凳子,增加的高度是相同的.
【测量整理】
叠放凳子的总高度$h$(cm)与凳子的数量$n$(个)的部分对应值如表:

【解决问题】
(1) 在图 2 中描出表中对应的点,并顺次连结各点.
(2) 根据图 2 中画出的图象确定符合实际的函数类型,求出$h$关于$n$的函数表达式.(不要求写自变量的取值范围)
(3) 若该超市的一位理货员将 10 个这种凳子叠放在一起,能否将其放入层高为 87 cm 的货架?请说明理由.


答案:
解析 (1)如图: ! (2)由图可知 h 是 n 的一次函数,设 h = kn + b(k ≠ 0),
把(2, 50),(3, 55)代入,得$\begin{cases}2k + b = 50 \\ 3k + b = 55\end{cases}$,解得$\begin{cases}k = 5 \\ b = 40\end{cases}$,
(2)由图可知 h 是 n 的一次函数,设 h = kn + b(k ≠ 0),
把(2, 50),(3, 55)代入,得$\begin{cases}2k + b = 50 \\ 3k + b = 55\end{cases}$,解得$\begin{cases}k = 5 \\ b = 40\end{cases}$,
∴ h 关于 n 的函数表达式为 h = 5n + 40。 (3)不能. 理由: 在 h = 5n + 40 中,令 n = 10,得 h = 5×10 + 40 = 90,
∵ 90>87,
∴ 将 10 个这种凳子叠放在一起,不能将其放入层高为 87 cm 的货架。
解析 (1)如图: !
 (2)由图可知 h 是 n 的一次函数,设 h = kn + b(k ≠ 0),
把(2, 50),(3, 55)代入,得$\begin{cases}2k + b = 50 \\ 3k + b = 55\end{cases}$,解得$\begin{cases}k = 5 \\ b = 40\end{cases}$,
(2)由图可知 h 是 n 的一次函数,设 h = kn + b(k ≠ 0),
把(2, 50),(3, 55)代入,得$\begin{cases}2k + b = 50 \\ 3k + b = 55\end{cases}$,解得$\begin{cases}k = 5 \\ b = 40\end{cases}$,∴ h 关于 n 的函数表达式为 h = 5n + 40。 (3)不能. 理由: 在 h = 5n + 40 中,令 n = 10,得 h = 5×10 + 40 = 90,
∵ 90>87,
∴ 将 10 个这种凳子叠放在一起,不能将其放入层高为 87 cm 的货架。
查看更多完整答案,请扫码查看


