《2025年5年中考3年模拟八年级数学下册华师大版》

7.（2024山东聊城月考）如图，A，B是双曲线$y = \frac{k}{x}(x ＞ 0)$上的两点，连结OA，OB.过点A作$AC\perp x$轴于点C，交OB于点D，若D为AC的中点，$\triangle AOD$的面积为3，点B的坐标为$(m,2)$，则m的值为（ ）

A.3
B.4
C.6
D.8

答案： **C**：因为 D 为 AC 的中点，$\triangle AOD$ 的面积为 3，所以 $\triangle AOC$ 的面积为 6，所以 k = 12，所以双曲线解析式为 $y = \frac{12}{x}$，把 B(m,2)代入 $y = \frac{12}{x}$，得 m = 6。故选 C。

8.（2024吉林长春朝阳模拟）如图，点A在反比例函数$y = \frac{8}{x}$的图象上，点B在反比例函数$y = \frac{k}{x}(k ＜ 0)$的图象上，连结AB，且$AB// x$轴，点$P(\frac{2}{3},0)$是x轴上一点，连结PA，PB，若$S_{\triangle APB} = 6$，则$k =$_______.

答案： **答案**：@@ **解析**：如图，连结 OA、OB，令 AB 交 y 轴于点 E，因为 AB//x 轴，所以 $S_{\triangle AOB}=S_{\triangle APB}=6$，因为点 A 在反比例函数 $y = \frac{8}{x}$ 的图象上，所以 $S_{\triangle AOE}=\frac{1}{2}×8 = 4$，所以 $S_{\triangle BOE}=6 - 4 = 2$，因为 $S_{\triangle BOE}=\frac{|k|}{2}=-\frac{k}{2}$，所以 k = -4。

9.（2023吉林第二实验学校一模）如图所示的是反比例函数$y = \frac{k_1}{x}$和$y = \frac{k_2}{x}(k_1 ＜ k_2)$在第一象限的图象，直线$AB// x$轴，并分别交两条双曲线于A、B两点，若$S_{\triangle AOB} = 2$，则$k_2 - k_1$的值是_______.

答案： **答案**：@@ **解析**：设 A(a,b)，B(c,d)，则 $k_1 = ab$，$k_2 = cd$，因为 $S_{\triangle AOB}=2$，所以 $\frac{1}{2}cd-\frac{1}{2}ab = 2$，所以 cd - ab = 4，所以 $k_2 - k_1 = 4$。

10.某反比例函数图象如图所示，已知点A在该图象上，过点A作$AC\perp y$轴于点C，B为x轴上一点，连结AB和CB，若$S_{\triangle ABC} = 2$，求该反比例函数的表达式.

答案： **解析**：设反比例函数的表达式为 $y = \frac{k}{x}(k≠0)$，A 点的坐标为(a,b)，因为函数图象在第二、四象限，所以 k ＜ 0，k = ab，因为 $S_{\triangle ABC}=2$，所以 $\frac{1}{2}|a|\cdot b = 2$，所以 -ab = 4，所以 ab = -4，即 k = -4，所以此函数的表达式为 $y = -\frac{4}{x}$。

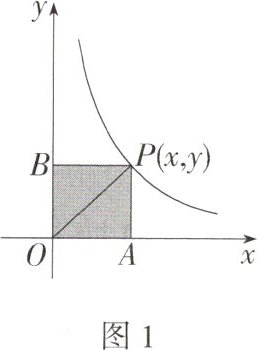
11.（1）如图1，过反比例函数$y = \frac{k}{x}(x ＞ 0)$图象上任意一点$P(x,y)$分别向x轴、y轴作垂线，垂线段分别为PA、PB，证明：$S_{长方形OAPB} = k$，$S_{\triangle OAP} = \frac{1}{2}k$，$S_{\triangle OPB} = \frac{1}{2}k$.
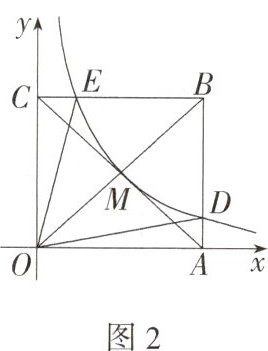
（2）如图2，反比例函数$y = \frac{k}{x}(x ＞ 0)$的图象经过长方形OABC对角线的交点M，分别与AB、BC交于点D、E，若四边形ODBE的面积为9，求k的值.

答案： **解析** - （1）证明：因为点 P(x,y)在反比例函数 $y = \frac{k}{x}(x＞0)$ 的图象上，所以 xy = k，因为 PA⊥x 轴，PB⊥y 轴，所以四边形 OAPB 是长方形，所以 PB = OA = x，OB = AP = y，所以 $S_{长方形OAPB}=OA\cdot OB = xy = k$，$S_{\triangle OAP}=\frac{1}{2}OA\cdot AP=\frac{1}{2}xy=\frac{1}{2}k$，$S_{\triangle OPB}=\frac{1}{2}PB\cdot OB=\frac{1}{2}xy=\frac{1}{2}k$。 - （2）由题意得点 E、M、D 在反比例函数的图象上，则 $S_{\triangle OCE}=\frac{|k|}{2}$，$S_{\triangle OAD}=\frac{|k|}{2}$，如图，过点 M 作 MG⊥y 轴于点 G，作 MN⊥x 轴于点 N，则 $S_{长方形ONMG}=|k|$，又因为 M 为长方形 OABC 对角线的交点，所以 $S_{长方形OABC}=4S_{长方形ONMG}=4|k|$，因为函数图象在第一象限，所以 k ＞ 0，所以 $\frac{k}{2}+\frac{k}{2}+9 = 4k$，解得 k = 3。