《2025年学霸提优大试卷四年级数学下册人教版》

4. 如图是由三个大小不同的等边三角形构成的。小蚂蚁从A地到B地，哪一条路线最近? 为什么? (6分)

答案： 中间一条路线最近 三个三角形都是等边三角形，中间一条路线的距离：$60 + 30 = 90(\text{cm})$，下面一条路线的距离：$60\times2 + 30\times2 = 180(\text{cm})$，上面一条路线的距离：$90\times2 = 180(\text{cm})$。$90＜180$，所以中间一条路线最近。

5. 一块三角形菜地，最大角的度数是最小角的3倍，另一个角的度数是最小角的2倍。这个三角形是什么三角形? 三个角的度数分别是多少度? (6分)

答案： $180^{\circ}\div(3 + 2 + 1)=30^{\circ}$ $30^{\circ}\times2 = 60^{\circ}$ $30^{\circ}\times3 = 90^{\circ}$ 答：这个三角形是直角三角形，三个角的度数分别是$90^{\circ}$、$60^{\circ}$、$30^{\circ}$。

1. 如图，AB = 6cm，BC = 2cm，AD = 9cm，CD = 3cm，AC长度是整厘米数，你知道AC的长度是多少吗? (5分)

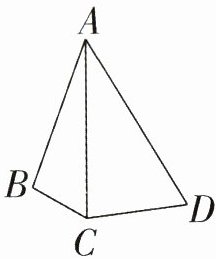
答案： 根据三角形的三边关系，在三角形$ABC$中，$AC$的长度可以是 5 cm、6 cm、7 cm；在三角形$ACD$中，$AC$的长度可以是 7 cm、8 cm、9 cm、10 cm、11 cm，所以$AC$的长度是 7 cm。
提示：利用三角形三边的关系，三角形任意两边之和大于第三边，任意两边之差小于第三边。在三角形$ABC$中，$AC$的长度可以是 5 cm、6 cm、7 cm；在三角形$ACD$中，$AC$的长度可以是 7 cm、8 cm、9 cm、10 cm、11 cm，所以符合条件的$AC$长度是 7 cm。

2. 如图，在三角形ABC中，点D在BC上，且∠1 = ∠2，∠3 = ∠4，∠5 = 24°，则∠1是多少度? (5分)

答案： $\angle 3+\angle 6 = 180^{\circ}$ $\angle 1+\angle 5+\angle 6 = 180^{\circ}$ $\angle 1+\angle 5=\angle 3=\angle 4$ $\angle 1=\angle 2$，$\angle 4=\angle 1+\angle 5$ $\angle 1+\angle 2+\angle 4+\angle 5 = 180^{\circ}$ $\angle 5 = 24^{\circ}$ $\angle 1+\angle 1+\angle 1+24^{\circ}+24^{\circ}=180^{\circ}$ $\angle 1 = 44^{\circ}$
提示：根据三角形内角和为$180^{\circ}$求解。$\angle 3+\angle 6 = 180^{\circ}$，$\angle 5 = 24^{\circ}$，所以$180^{\circ}-\angle 3 = 180^{\circ}-(\angle 1+\angle 5)$，即$\angle 3=\angle 1+24^{\circ}$。因为$\angle 3=\angle 4$，所以$\angle 4=\angle 1+24^{\circ}$。因为$\angle 1=\angle 2$，所以$\angle 1+\angle 2+\angle 4+\angle 5=\angle 1+\angle 1+\angle 1+24^{\circ}+24^{\circ}=180^{\circ}$，所以$\angle 1 = 44^{\circ}$。

一 填空题。(每空1分,共24分)
1. 0.9加上(　　　)个0.1是1；0.53加上(　　　)个0.01是0.63。

答案：  1 10

2. 8个0.1与80个0.01的和是(　　　)。

答案：  1.6

3. 5.9+7.86+4.1 = 5.9+(　　　)+7.86，这是运用了加法(　　　)律。

答案： 4.1 交换

4. 最小的两位数比最小的两位小数多(　　　)。

答案： 9.99

5. 比4.7多2.8的数是(　　　)；比13.9少(　　　)的数是6.5。

答案：  7.5 7.4

6. 1.5去掉小数点后比原数大(　　　)。

答案： 13.5

7. 在〇里填上“＞”“＜”或“=”。
0.8+1〇0.9 10−9.9〇1
1.49+7.8〇7.8+1.49 9.1−3.67〇9.1−3.76
0.8+2〇8.2 0.9+0.99〇2−0.11

答案：  ＞ ＜ = ＞ ＜ =

8. 世界上最小的奶牛是一种叫“维丘奶牛”的印度瘤牛，它的身高只有0.81m。这个数至少加上(　　　)就等于一个整数。

答案：  0.19

9. 找规律填数。
(1)1.8，2.5，3.2，(　　　)，(　　　)。
(2)0.4，0.48，0.56，(　　　)，(　　　)。
(3)新趋势 推导探究 根据前三题的结果，直接写出得数。
1.2+1.12 = 2.32
1.2+1.12+1.112 = 3.432
1.2+1.12+1.112+1.1112 = 4.5432
1.2+1.12+1.112+1.1112+1.11112 = (　　　　　　　　　　)
1.2+1.12+1.112+…+1.$\underbrace{1\cdots1}_{7个1}$2 = (　　　　　　　　　　　　)

答案：
(1)3.9 4.6
(2)0.64 0.72
(3)5.65432 8.98765432

10. 为测量池塘水深，将一根长3m的竹竿垂直插入池塘，发现竹竿入泥部分长13cm，露出水面部分长45cm，该池塘水的深度是(　　　)m。
11. 小凯在计算1.39加上一个一位小数时，错误地把数的末尾对齐，结果得到1.84。正确的得数是(　　　)。

答案：  2.42 11. 5.89