《2025年海淀单元测试AB卷六年级数学下册青岛版》

10. 有一块棱长为 5 分米的正方体木料，把这块木料加工成一个最大的圆柱，要削去（ ）dm³的木料。

答案： 26.875 [解析]削去木料的体积 = 正方体体积 - 圆柱体积，即$5×5×5 - 3.14×(5÷2)^2×5 = 26.875(dm^3)$。

二 准确判断。（对的画“√”，错的画“×”）（10 分）
1. 圆柱的侧面展开图一定是一个正方形。（ ）
2. 一个圆柱的高与它底面圆的半径长度相等，那么圆柱的侧面积等于两个底面积的和。（ ）
3. 圆锥的体积扩大到原来的 3 倍，它就变成了圆柱。（ ）
4. 如果圆锥的体积等于圆柱体积的$\frac{1}{3}$，那么圆柱和圆锥一定等底等高。（ ）
5. 把一个圆柱平均截成两个小圆柱，那么每个小圆柱的表面积是原来大圆柱表面积的$\frac{1}{2}$。（ ）

答案： 1. × 2. √ 3. × 4. × 5. × [解析]切割后的小圆柱的侧面积是原圆柱的侧面积的一半，而小圆柱的底面积等于原圆柱的底面积，所以小圆柱的表面积是原来大圆柱表面积的$\frac{1}{2}$，再加上1个底面积，所以原题说法错误。

三 择优选择。（把正确答案的字母填在括号里）（15 分）
1. **辨思维** **易错题**把一个圆柱形木块削成一个最大的圆锥，需要削去部分的体积是原来圆柱形木块体积的（ ）。
A. $\frac{1}{3}$ B. $\frac{2}{3}$ C.无法确定

答案： 1. B 

2. **新素养** **几何直观**在庆祝六一儿童节美术作品征集活动中，乐乐准备制作一个创意笔筒，他用彩纸给笔筒侧面围一圈装饰图（接口处不计），用下面（ ）种彩纸最合适。

答案： 2. B

3. 一个圆柱与一个圆锥的底面直径相等，圆锥的高是圆柱的 3倍，如果圆锥的体积是12立方分米，那么圆柱的体积是（ ）立方分米。
A.12 B.36 C.4

答案：  3. A

4.如图，把等腰三角形绕它的底边上的高旋转一周，得到的立体图形的体积是（ )cm³。

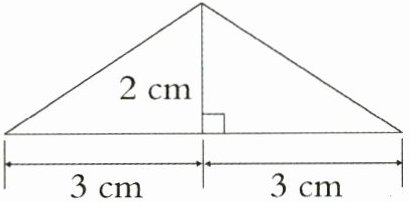
A.56.52 B.25.12 C.18.84

答案：  4. C 

5.如图是两位同学对同一个圆柱的两种不同的切分方法(都是平均分成两部分)。甲同学切分后，表面积比原来增加了( )；乙同学切分后,表面积比原来增加了( )。

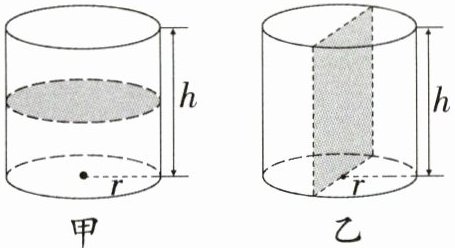
A.$2\pi r^{2}$ B.$4rh$ C.$2rh$

答案： 5. A B [解析]甲同学切分方法是把圆柱切分成两部分后，表面积增加了2个圆柱的底面积；乙同学切分方法是把圆柱切分成两部分后，表面积增加了2个以圆柱的高为长、直径为宽的长方形的面积。