《2025年一本初中数学九年级下册华师大版》

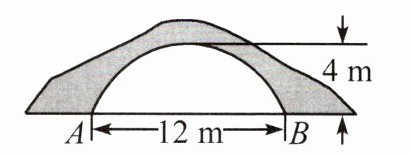
11.一座拱桥的截面如图所示.当水面宽$AB$为$12\ m$时，桥洞顶部离水面$4\ m$，已知桥洞的拱形是抛物线，以水平方向为$x$轴，建立平面直角坐标系，若选取点$A$为坐标原点时的抛物线表达式为$y=-\frac{1}{9}(x - 6)^{2}+4$，则选取点$B$为坐标原点时的抛物线表达式为____________.

答案： $y = -\frac{1}{9}(x + 6)^{2}+4$

12.已知二次函数图象的顶点在$x$轴上，且图象经过点$(2,-2)$和$(-1,-8)$，则该二次函数的表达式为________________.

答案： $y = -2(x - 1)^{2}$或$y = -\frac{2}{9}(x - 5)^{2}$

13.(2024·自贡期末)如图，九(1)班劳动实践基地位于$L$形围墙的内侧，已知$\angle ABC = 90^{\circ}$，墙$AB$长$7\ m$，$BC$长$3\ m$.同学们准备用$10\ m$长的围栏在基地内围出一块矩形菜地（可利用围墙），他们能围出的最大面积是_____$m^{2}$.

答案： 21

14.(2024·南充)2024年“五一”假期期间，阆中古城景区某特产店销售$A,B$两类特产.$A$类特产进价$50$元/件，$B$类特产进价$60$元/件.已知购买$1$件$A$类特产和$1$件$B$类特产需$132$元，购买$3$件$A$类特产和$5$件$B$类特产需$540$元.
(1)求每件$A$类特产和$B$类特产的售价各是多少元.
(2)$A$类特产供货充足，按原价销售每天可售出$60$件.市场调查反映，若每降价$1$元，每天可多售出$10$件（每件售价不低于进价）.设每件$A$类特产降价$x$元，每天的销售量为$y$件，求$y$与$x$的函数关系式，并写出自变量$x$的取值范围.
(3)在(2)的条件下，由于$B$类特产供货紧张，每天只能购进$100$件且按原价售完.设该店每天销售这两类特产的总利润为$w$元，求$w$与$x$的函数关系式，并求出当每件$A$类特产降价多少元时总利润$w$最大，最大利润是多少元.（利润 = 售价 - 进价）

答案：
(1)每件A类特产的售价为60元，每件B类特产的售价为72元
(2)$y = 60 + 10x(0\leqslant x\leqslant 10)$
(3)w与x的函数关系式为$w = -10(x - 2)^{2}+1840$，当每件A类特产降价2元时，总利润w最大，最大利润是1840元

15.求二次函数$y=-x^{2}+(m - 1)x + m$.
(1)求证：不论$m$取何值，该函数图象与$x$轴总有公共点.
(2)若该函数的图象与$y$轴交于点$(0,3)$，求出顶点坐标并画出该函数图象.
(3)在(2)的条件下，观察图象.
①不等式$-x^{2}+(m - 1)x + m＞3$的解集是__________；
②若一元二次方程$-x^{2}+(m - 1)x + m = k$有两个不相等的实数根，则$k$的取值范围是________；
③若一元二次方程$-x^{2}+(m - 1)x + m - t = 0$在$-1＜x＜4$的范围内有实数根，则$t$的取值范围是___________.

答案： 解：
(1)证明：$\because\Delta = b^{2}-4ac=(m - 1)^{2}-4\times(-1)\times m=(m + 1)^{2}\geqslant0$， $\therefore$不论m取何值，该函数图象与x轴总有公共点.
(2)顶点坐标为(1,4)，该函数图象略
(3)$0＜x＜2$ $k＜4$ $-5＜t\leqslant4$