《2025年一本初中数学九年级下册华师大版》

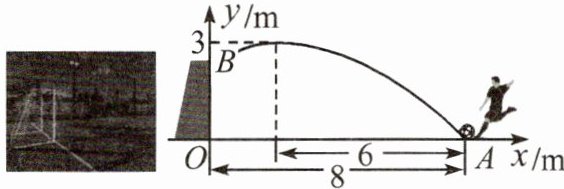
4.（2023·温州）一次足球训练中，小明从球门正前方 8 m 的 $ A $ 处射门，球射向球门的路线呈抛物线形. 当球飞行的水平距离为 6 m 时，球达到最高点，此时球离地面 3 m. 已知球门高 $ OB $ 为 2.44 m，现以 $ O $ 为原点建立如图所示的平面直角坐标系.
（1）求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）；
（2）对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则他应该带球向正后方移动多少米射门，才能让足球经过点 $ O $ 正上方 2.25 m 处？

答案： 解：
(1) $\because 8 - 6 = 2$，$\therefore$ 抛物线的顶点坐标为 $(2,3)$。 设抛物线的函数表达式为 $y = a(x - 2)^{2}+3$。 把点 $A(8,0)$ 代入，得 $36a + 3 = 0$，解得 $a = -\frac{1}{12}$， $\therefore$ 抛物线的函数表达式为 $y = -\frac{1}{12}(x - 2)^{2}+3$。 当 $x = 0$ 时，$y = -\frac{1}{12}\times4 + 3=\frac{8}{3}＞2.44$， $\therefore$ 球不能射进球门。@@
(2) 设小明带球向正后方移动 $b\ m$，则移动后的抛物线为 $y = -\frac{1}{12}(x - 2 - b)^{2}+3$。 把点 $(0,2.25)$ 代入，得 $2.25 = -\frac{1}{12}(0 - 2 - b)^{2}+3$， 解得 $b = -5$（舍去）或 $b = 1$， $\therefore$ 他应该带球向正后方移动 1 m 射门，才能让足球经过点 $O$ 正上方 2.25 m 处。

5.（2024·内江）端午节吃粽子是中华民族的传统习俗. 市场上猪肉粽的进价比豆沙粽的进价每盒多 20 元，某商家用 5 000 元购进的猪肉粽盒数与 3 000 元购进的豆沙粽盒数相同. 在销售中，该商家发现猪肉粽每盒售价 52 元时，可售出 180 盒；每盒售价每提高 1 元，就少售出 10 盒.
（1）求每盒猪肉粽、豆沙粽的进价；
（2）设每盒猪肉粽的售价为 $ x $（$52\leqslant x\leqslant70$）元，该商家销售猪肉粽的利润为 $ y $（单位：元），求 $ y $ 关于 $ x $ 的函数表达式，并求出 $ y $ 的最大值.

答案： 解：
(1) 设每盒猪肉粽的进价为 $a$ 元，则每盒豆沙粽的进价为 $(a - 20)$ 元。 由题意，得 $\frac{5000}{a}=\frac{3000}{a - 20}$，解得 $a = 50$。 经检验，$a = 50$ 是方程的解，此时 $a - 20 = 30$， $\therefore$ 每盒猪肉粽的进价为 50 元，每盒豆沙粽的进价为 30 元。@@
(2) 由题意可知，当每盒猪肉粽的售价为 $x$ 元时，每天可售 $[180 - 10(x - 52)]$ 盒， $\therefore y=(x - 50)[180 - 10(x - 52)]=-10x^{2}+1200x - 35000=-10(x - 60)^{2}+1000$。 $\because -10 ＜ 0$，$52\leqslant x\leqslant70$， $\therefore$ 当 $x = 60$ 时，$y$ 取最大值，最大值为 1000。 故 $y$ 关于 $x$ 的函数表达式为 $y = -10x^{2}+1200x - 35000(52\leqslant x\leqslant70)$，$y$ 的最大值为 1000。