2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列说法中,正确的是 (
A.数列2,4,6,8可表示为集合$\{2,4,6,8\}$
B.数列1,2,3,4与数列4,3,2,1是相同的
数列
C.数列$\{n^2 + n\}$的第$k$项为$k^2 + k$
D.数列0,1,2,3,4,…可记为$\{n\}$
C
)A.数列2,4,6,8可表示为集合$\{2,4,6,8\}$
B.数列1,2,3,4与数列4,3,2,1是相同的
数列
C.数列$\{n^2 + n\}$的第$k$项为$k^2 + k$
D.数列0,1,2,3,4,…可记为$\{n\}$
答案:
1.C 对于A,由数列的定义易知A错误;对于B,两个数列排列次序不同,是不同的数列,故B错误;对于C,数列$\{n^2 + n\}$的第k项为$k^2 + k$,故C正确;易知D错误.
2. (2025·河北保定期末)数列$2^5$,$2^8$,$2^{11}$,…,$2^{3n + 11}(n \in \mathbf{N}^*)$的项数是 (
A.$3n + 11$
B.$n + 4$
C.$n + 3$
D.$n$
C
)A.$3n + 11$
B.$n + 4$
C.$n + 3$
D.$n$
答案:
2.C 5,8,11的间隔是3,若$n = 1$,则$3n + 11 = 14$,所以数列的项数为$n + 3$.
3. 数列$-2$,$\frac{4}{3}$,$-\frac{6}{5}$,$\frac{8}{7}$,…的通项公式可以为 (
A.$a_n = (-1)^n \frac{n}{2n + 1}$
B.$a_n = (-1)^n \frac{2n}{2n - 1}$
C.$a_n = (-1)^{n - 1} \frac{2n}{2n + 1}$
D.$a_n = (-1)^{n + 1} \frac{2n}{2n - 1}$
B
)A.$a_n = (-1)^n \frac{n}{2n + 1}$
B.$a_n = (-1)^n \frac{2n}{2n - 1}$
C.$a_n = (-1)^{n - 1} \frac{2n}{2n + 1}$
D.$a_n = (-1)^{n + 1} \frac{2n}{2n - 1}$
答案:
3.B 对于选项A:令$n = 1$,可得$a_1 = -\frac{1}{3}$,不符合题意;对于选项B:代入检验均可,符合题意;对于选项C:令$n = 1$,可得$a_1 = \frac{2}{3}$,不符合题意;对于选项D:令$n = 1$,可得$a_1 = 2$,不符合题意.故选B.
4. 已知数列$\{a_n\}$满足$a_n = \begin{cases}n + 1, n \leq 3, \\ 2n, n > 3\end{cases}(n \in \mathbf{N}^*)$,且$a_n = 4$,那么$n$等于 ( )
A.2
B.3
C.4
D.2或3
A.2
B.3
C.4
D.2或3
答案:
4.B 由题设,若$a_n = n + 1 = 4$,可得$n = 3 \in \{n|n \leq 3, n \in \mathbf{N}^*\}$,若$a_n = 2n = 4$,可得$n = 2 \notin \{n|n > 3, n \in \mathbf{N}^*\}$,所以$n = 3$.
5. (多选)已知数列$1$,$\sqrt{2} + 1$,$\sqrt{3} + \sqrt{2}$,$2 + \sqrt{3}$,…,$\sqrt{n} + \sqrt{n - 1}$,…,则下列说法正确的是 (
A.$3 + 2\sqrt{2}$是它的第3项
B.$4 + \sqrt{15}$是它的第4项
C.$3 + 2\sqrt{2}$是它的第9项
D.$4 + \sqrt{15}$是它的第16项
CD
)A.$3 + 2\sqrt{2}$是它的第3项
B.$4 + \sqrt{15}$是它的第4项
C.$3 + 2\sqrt{2}$是它的第9项
D.$4 + \sqrt{15}$是它的第16项
答案:
5.CD 当$n = 9$时,$\sqrt{n} + \sqrt{n - 1} = 3 + 2\sqrt{2}$,故C正确,A错误;当$n = 16$时,$\sqrt{n} + \sqrt{n - 1} = 4 + \sqrt{15}$,故D正确,B错误.
6. (多选)数列2,0,2,0,…的通项公式可以是 (
A.$a_n = (-1)^{n + 1} + 1$
B.$a_n = (-1)^n + 1$
C.$a_n = 2\left| \sin \frac{n\pi}{2} \right|$
D.$a_n = \begin{cases} 2, n = 1, \\ 2 - a_{n - 1}, n \geq 2 \end{cases}$
ACD
)A.$a_n = (-1)^{n + 1} + 1$
B.$a_n = (-1)^n + 1$
C.$a_n = 2\left| \sin \frac{n\pi}{2} \right|$
D.$a_n = \begin{cases} 2, n = 1, \\ 2 - a_{n - 1}, n \geq 2 \end{cases}$
答案:
6.ACD 对于A:当$n$为奇数时,$a_n = 1 + 1 = 2$,当$n$为偶数时,$a_n = -1 + 1 = 0$,故A正确;对于B:当$n$为奇数时,$a_n = -1 + 1 = 0$,当$n$为偶数时,$a_n = 1 + 1 = 2$,故B错误;对于C:当$n$为奇数时,设$n = 2k - 1, k \in \mathbf{Z}$,则$a_n = 2\left|\sin\frac{(2k - 1)\pi}{2}\right| = 2\left|\sin\left(k\pi - \frac{\pi}{2}\right)\right| = 2\left|\sin\frac{\pi}{2}\right| = 2$,当$n$为偶数时,设$n = 2k, k \in \mathbf{Z}$,则$a_n = 2\left|\sin\frac{2k\pi}{2}\right| = 2|\sin k\pi| = 0$,故C正确;对于D:易知$a_1 = 2, a_2 = 2 - a_1 = 0$,当$n \geq 2$时,$a_n + a_{n - 1} = 2$,用$n + 1$代替$n$,可得$a_{n + 1} + a_n = 2$,两式相减得$a_{n + 1} - a_{n - 1} = 0$,所以数列$\{a_n\}$的奇数项、偶数项分别相等,故D正确.
7. 已知数列$\{a_n\}$的通项公式为$a_n = n^2 + 2n$,若第$2m$项是第$m$项的3倍,则$m =$
2
.
答案:
7.2 解析 由题得$a_{2m} = 3a_m$,又$a_{2m} = 4m^2 + 4m$,$a_m = m^2 + 2m$,所以$4m^2 + 4m = 3m^2 + 6m$,解得$m = 0$(舍去)或$m = 2$.
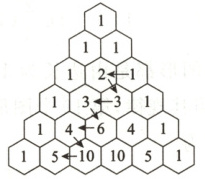
8. 如图所示,从1开始箭头所指的数组成一个锯齿形数列:1,2,3,3,6,4,10,5,…,则在该数列中第37项是
190
.
答案:
8.190 解析 由题意可得第4,5,6行的第三个数依次为$3 = 1 + 2$,$6 = 1 + 2 + 3$,$10 = 1 + 2 + 3 + 4$,所以第$k(k \geq 4)$行的第三个数为$1 + 2 + ·s + (k - 2)$,在该数列中,第37项为第21行第三个数,所以该数列的第37项为$1 + 2 + ·s + 19 = \frac{19 × (19 + 1)}{2} = 190$.
9. 写出下列数列的一个通项公式.
(1)0,3,8,15,24,…;
(2)1,$-3$,5,$-7$,9,…;
(3)$0$,$\frac{2^2 - 2}{5}$,$\frac{3^2 - 3}{10}$,$\frac{4^2 - 4}{17}$,…;
(4)1,11,111,1 111,….
(1)0,3,8,15,24,…;
(2)1,$-3$,5,$-7$,9,…;
(3)$0$,$\frac{2^2 - 2}{5}$,$\frac{3^2 - 3}{10}$,$\frac{4^2 - 4}{17}$,…;
(4)1,11,111,1 111,….
答案:
9.解
(1)观察数列中的数,可以看到$0 = 1 - 1$,$3 = 4 - 1$,$8 = 9 - 1$,$15 = 16 - 1$,$24 = 25 - 1$,$·s$,所以它的一个通项公式是$a_n = n^2 - 1$.
(2)数列各项的绝对值为$1,3,5,7,9,·s$,是连续的正奇数,并且数列的奇数项为正,偶数项为负,所以它的一个通项公式为$a_n = (-1)^{n + 1}(2n - 1)$.
(3)因为$5 = 2^2 + 1$,$10 = 3^2 + 1$,$17 = 4^2 + 1$,所以数列的一个通项公式为$a_n = \frac{n^2 - n}{n^2 + 1}$.
(4)原数列的各项可变为$\frac{1}{9}$,$\frac{1}{9} × 9$,$\frac{1}{9} × 99$,$\frac{1}{9} × 999$,$\frac{1}{9} × 9999$,$·s$,易知数列$9,99,999,9999,·s$的一个通项公式为$10^n - 1$,所以原数列的一个通项公式为$a_n = \frac{1}{9}(10^n - 1)$.
(1)观察数列中的数,可以看到$0 = 1 - 1$,$3 = 4 - 1$,$8 = 9 - 1$,$15 = 16 - 1$,$24 = 25 - 1$,$·s$,所以它的一个通项公式是$a_n = n^2 - 1$.
(2)数列各项的绝对值为$1,3,5,7,9,·s$,是连续的正奇数,并且数列的奇数项为正,偶数项为负,所以它的一个通项公式为$a_n = (-1)^{n + 1}(2n - 1)$.
(3)因为$5 = 2^2 + 1$,$10 = 3^2 + 1$,$17 = 4^2 + 1$,所以数列的一个通项公式为$a_n = \frac{n^2 - n}{n^2 + 1}$.
(4)原数列的各项可变为$\frac{1}{9}$,$\frac{1}{9} × 9$,$\frac{1}{9} × 99$,$\frac{1}{9} × 999$,$\frac{1}{9} × 9999$,$·s$,易知数列$9,99,999,9999,·s$的一个通项公式为$10^n - 1$,所以原数列的一个通项公式为$a_n = \frac{1}{9}(10^n - 1)$.
查看更多完整答案,请扫码查看


